Boolean algebra is derived from algebra which is one of the major branches of mathematics. There are so many branches of mathematics such as calculus, arithmetic, algebra, geometry, numerical analysis etc., which are further elaborated into different categories. These branches are used in almost every field and have different methods to solve their related problems.
To discuss about Boolean algebra, we just go through with its main branch i.e., Algebra. There are five different types of Algebra which are as follow:
- Abstract Algebra
This type of algebra is used to solve the concepts regarding sets, binary operations, associativity, identity elements & inverse elements.
- Advanced Algebra
This branch will help you to solve the problems regarding equations with inequalities, conic sections, polynomial equation, sequences & series, matrices, quadratic functions with inequalities, rational expressions etc.
- Elementary Algebra
It covers the concepts including evaluating expressions and equations, variables, properties of inequalities and equalities etc.
- Linear Algebra
The topics including vector spaces, relations and computations, linear equations and matrices & matrix decomposition are dealt with under this branch.
- Communicative Algebra
This branch studies about algebraic number theory, algebraic geometry etc.
Index
Define Boolean algebra
Boolean algebra deals with the operations on logical values and its variable values are only truth values i.e., true and false. Generally, It is denoted by 1 and 0. Boolean algebra is also called logical algebra or binary algebra and it exists in the main branch of Abstract Algebra.
Operations performed on Boolean algebra
The following are the basic operations which are performed on Boolean algebra:
- NOT Operation
- OR Operation
- AND Operation
Not operations is also called negation and represented as ¬ or !
OR operation is known as Disjunction and represented as ∨ or I I
Where
AND operation is also defined as Conjunction and represented as ∧ or &&
Graphical Representation of Boolean algebraic operations
Boolean algebra operations can be represented by Venn Diagram by shading overlapping region.
Venn diagram representing conjunction, disjunction and negation is as under:
Boolean Expressions:
Boolean expressions are logical statements that are written with logical operators.
For example:
X OR Y
A AND B
(Here OR & AND are logical operators)
Truth Table:
Truth table provides all possible logical values of logical variables and their combinations.
| A | B | A ∨ B | A ∧ B |
| True (1) | True (1) | True (1) | True (1) |
| True (1) | False (0) | True (1) | False (0) |
| False (0) | True (1) | True (1) | False (0) |
| False (0) | False (0) | False (0) | False (0) |
| A | ¬A |
| True (1) | False (0) |
| False (0) | True (1) |
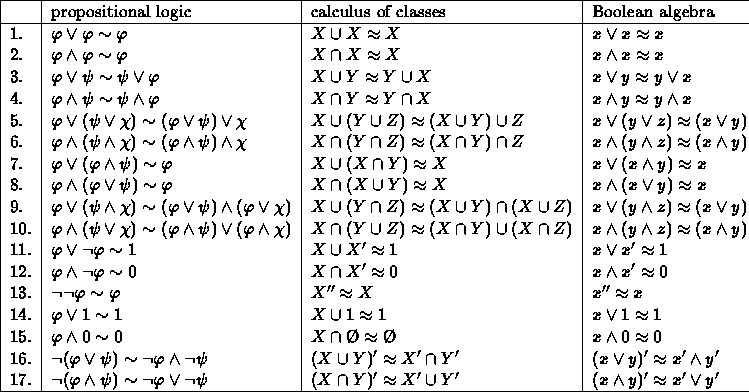
Laws of Boolean algebra
There are six Boolean algebra laws which are used to solve the Boolean algebraic expressions:
- AND Law
x . 0 = 0
x . 1 = x
x . x = x
x . x՟ = 0
- OR Law
x + 0 = x
x + 1 = 1
x + x = x
x + x՟ = 1
- Inversion Law
x + x̿ = 1
(It means the result of double inversion of a variable is the original variable.)
- Associative Law
(x . y) . z = x . (y . z)
(x + y) + z = x + (y + z)
- Distributive Law
x . (y . z) = (x . y) + (x . z)
x + (y . z) = (x + y) . (x . z)
- Commutative Law
x . y = y . x
x + y = y + x
Solution of Boolean Algebra Expressions by De Morgan’s Law:
The most widely used theorems to solve the Boolean algebra are De Morgan’s Laws. These are of two types: De Morgan’s First Law and De Morgan’s Second Law.
First law of De Morgan: (x . y)’ = x’ + y’
It states that the sum of their individual complement of a variable is equal to the complement of product of variable.
Truth table to verify De morgan First Law:
| x | y | x’ | y’ | (x . y)’ | x’ + y’ |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 |
Second Law of De Morgan: (x + y)’ = x’ . y’
It states that the complement of sum of the variable is equal to the product of their individual complement or vice versa.
Truth table to verify De Morgan Second Law:
| x | y | x’ | y’ | (x . y)’ | x’ + y’ |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
Boolean algebra expressions can be written in different forms and their result can be generated with truth tables by using a Boolean algebra calculator.
Example 1: Draw a Truth Table for x (y + z)
Solution:
Given expression is x (y + z)
| x | y | Z | y + z | x (y + z) |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 |
Example 2: Draw a truth table for (x + y) (x + z)
Solution:
Given is (x + y) (x + z)
| x | y | z | x + y | x + z | (x + y) (x + z) |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
You can verify this table using an online Boolean expression calculator.
