Arrhenius equation is an equation in chemistry that helps calculate how chemical reactions change their speed based on temperature.
Index
The Equation
The equation states that

Let us understand the terms involved:
- k is the rate constant, which tells how fast the reaction proceeds.
- A is the pre-exponential factor or probability factor or Arrhenius constant. In simple terms, it is the frequency of correctly oriented collisions between the reactants which lead to products.
- e is Euler’s number, which is an important mathematical number related to natural growth. It is approximately equal to 2.718.
- Ea is the activation energy of the reaction. In other words, it is the energy needed to be provided to make the reactants become products.
- R is the universal gas constant. It is equal to 8.314 J mol-1 K-1 in SI units.
- T is the temperature at which the reaction is taking place, in units Kelvin.
Implications of the Equation

In simplest terms, the equation means just this: the higher the temperature, the faster the reaction proceeds.
How do we understand this mathematically? In the equation, notice that an exponent is involved. All the terms (Ea, R, and T) involved in the exponent are positive, so the use of the negative sign outside makes the exponent negative.
The term involving temperature is in the denominator, which means that more temperature makes the exponent less negative. Because of a less negative exponent, the overall term involving the exponent becomes bigger, when the temperature rises.
Thus, the value of k also becomes more when the temperature increases. The equation proceeds faster.
Physical Interpretation

To understand the equation in a physically meaningful way, Arrhenius explained as follows. He assumed that the equation proceeds only when the reactants have an energy greater than the activation energy. The fraction of total particles that have this much energy can be obtained from the Maxwell-Boltzmann distribution, a distribution that has wide-ranging applications in statistical mechanics. This gives rise to the exponential term in the equation.
As for the pre-exponential factor A, Arrhenius explained it in terms of successful collisions between reactant molecules. It is a term that depends on the relative sizes of the reactant molecules and their ability to fit with each other.
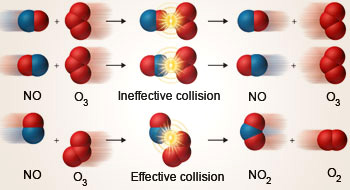
Applications
The Arrhenius equation has applications in many fields involving rates of reactions. For example, it can be used to predict how the rate of a reaction can be optimized by increasing temperature. This could be used to maximize the yield of products in given conditions.
It could also be used to calculate the activation energy of a reaction based on studies of rates of the reaction.
Conclusion
The Arrhenius equation is a very useful tool in modeling rates of reactions. Even though it is more of an empirical relation than a fundamental law, now from the standpoint of modern physical chemistry, it still is valuable in quick calculations.