Coulomb’s Law is a basic equation of electrostatics that explains how charged particles interact. It established the beginnings of the study of electromagnetism, in a quantitative form.
It is often the first piece of information that beginners to electrostatics learn. Its legacy is seen in some form or the other in most electrostatics problems.
Index
History
Coulomb’s law was arrived at by some experimental work by Charles-Augustin de Coulomb, a French physicist, in 1785. Others had already imagined the form of the equation, and perhaps even arrived at the final version independently.
Coulomb was the one who went on to publish it first, however, and his name thus is associated with it. He experimented with the forces between charged metal balls, at varying distances and charges, to arrive at the final result.
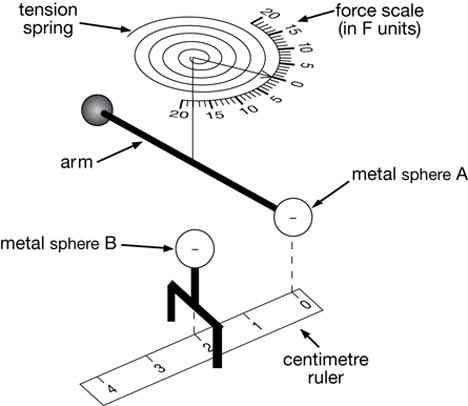
The Law
Coulomb’s law states that:
The magnitude of force between two spherically symmetric charges is directly proportional to the product of their charges. It is inversely proportional to the square of the distance between them. It is attractive if the charges are different, and repulsive if they are the same.
Mathematically, the magnitude of force is given by:
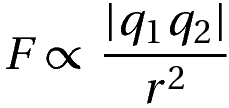
Where
F is the magnitude of the force
q1 and q2 are the magnitudes of charges
r is the distance separating them.
Eliminating the proportionality sign with the use of a proportionality constant, we get the equation for coulomb’s law.
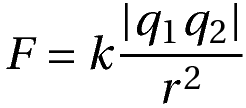
Where k must be obtained experimentally.
In SI units, k = 8.98 * 109 N m2 C-2. Also, k is written as
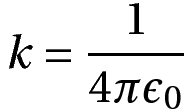
Where ϵ0 is the permittivity of free space.
We have coulomb’s law in vector form wherein the direction of the force is also specified.
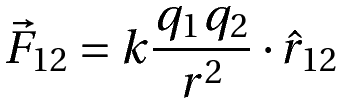
Where
F12 is the force on q1 due to q2
r12 is the vector pointing from q2 to q1.
r is the magnitude of the vector.
Extensions
Though it is defined only for spherically symmetric charges, Coulomb’s law can be extended to other charge distributions by using the principle of superposition. The principle basically states that when multiple charges are present, one can find the total force on anyone by vectorially adding the individual forces on it. In its most general form, an integral over space is obtained.
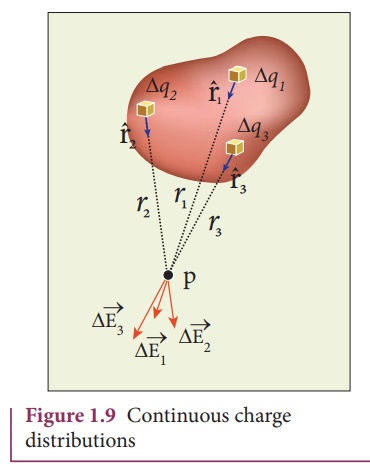
The force on a test charge, q, with a position vector r by a continuous distribution of charge is given by:
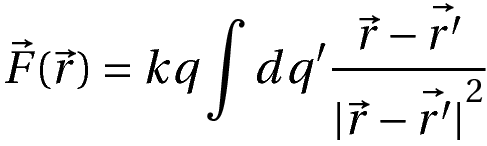
Where dq’ is each elementary charge and the corresponding position vector is r’.
In the discrete case, it is expressed as a sum, not an integral.
Limitations
When using Coulomb’s law, care has to be taken that all charges we are dealing with are point charges, or are dealt with suitably, in case of continuous charges. It is of special importance that the situation considered is static: none of the charges must be moving. If there is motion, magnetic forces get involved, which complicate matters. In that case, the situation is no longer of electrostatics and must be dealt with in electrodynamics.

