Fermat’s Last Theorem is one of the most intriguing problem of number theory. Legendary mathematician Pierre de Fermat stated it without any proof in 1637.
In its earliest form, it turned up scribbled in the margin of a mathematics book that Fermat was reading. But what does it say?
Fermat’s Last Theorem states that no three positive integers a, b, and c satisfy the equation aⁿ + bⁿ = cⁿ for any integer value of n greater than 2
It is among the most notable theorems in the history of mathematics. Prior to the proof it was in the Guinness Book of World Records as the “most difficult mathematical problem” because the theorem has the largest number of unsuccessful proofs.
Index
Implications
The equation says that when n is 1 or 2, we can have solutions that are natural numbers, that is, counting numbers like 1, 2, 3, and so on. This is easy to verify.
When n=1. The equation is simply
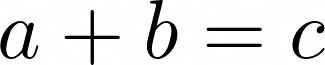
We can always find three integers that fit this. For example, a = 10, b = 5 and c = 15 satisfies this equation. There are actually infinitely many such solutions, as we can intuitively see.
When n = 2, the equation becomes:
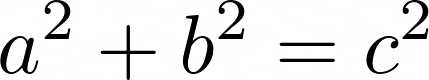
While this is not as intuitive as the first case, it still has infinitely many natural number solutions. For example, a = 3, b = 4, and c = 5 satisfies this equation, because, 3^2 = 9, 4^2 = 16, and 9+16 = 25, which is equal to 5^2.
Now, what about the cases with n more than 2? Are there natural number solutions for n = 3, that is,
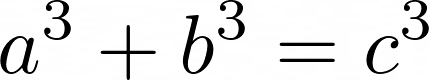
What about n = 4? n =5? n = 1001?
Early History
As we’ve already seen, people had already known the solutions for cases of n = 1 and n = 2. But to prove Fermat’s Last Theorem, there should be no natural numbers a,b, and c that satisfy the equation for n more than 2. How do we prove that?
Fermat himself claimed to have a proof, in his scribbling in the margins of the book. Quoting him,
It is impossible to separate a cube into two cubes, or a fourth power into two fourth powers, or in general, any power higher than the second, into two like powers. I have discovered a truly marvelous proof of this, which this margin is too narrow to contain.

What was this proof?
No mathematicians knew of it, nor did Fermat ever publish any such that. His claim came to be known as Fermat’s Conjecture because it was not yet proven then. It gained publicity after his death and became a quest of sorts for mathematicians.
Attempting Specific Cases
Most early mathematicians who worked on Fermat’s Conjecture proved specific cases of n. For example, Fermat himself tackled the case of n = 4, proving that there are no natural numbers a, b, and c, that satisfy
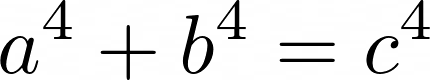
This was a helpful step going forth because it meant that mathematicians did not have to prove Fermat’s Conjecture for all numbers now. They only had to do so for odd prime numbers, the remaining would follow from the previous result and simple laws of exponents.
The first odd prime to be tackled was 3. Euler provided an almost complete proof for n=3 in 1770 and a few others corrected it in the early 19th century.
Next up was n = 5, proved separately by the 19th century mathematicians Adrien-Marie Legendre and Peter Dirichlet in 1825.
Gabriel Lamé showed the case for n = 7 in 1839. Others developed a simplified proof later.
Though the proof was now required only for odd primes, others still tried working with even numbers, such as n = 6, 10, and 14. Their proofs were different in approach and structure from the proof for odd numbers and did provide mathematicians with new insights.
Problems With the Specific Approach
While dealing with each case separately was giving results, the progress was very slow. The highest value of n for which Fermat’s Conjecture was proved was 14. The highest odd prime value was only n = 7. Unfortunately, this meant little, because, Fermat’s Conjecture had to be proven for all natural numbers n. At the rate at which the proofs were progressing, this would take forever.
Furthermore, the different proofs for different n showed little or no similarity. If there was some common theme, mathematicians might have been able to get an idea for a general proof for all n. But that was not the case so far. The proofs were simply getting more and more complicated with larger values of n.
Towards a General Proof
Sophie Germain, a mathematician from France, took the first steps for a general proof. She was self-taught, without the access to formal education which other mathematicians of her age had. She suggested ideas based on modular arithmetic and number theory, to arrive at a proof for all values of n.
Unfortunately, such a proof could not exist because of mathematical requirements, but the ideas she had set mathematicians on the right track. They began looking for more general ways to prove the theorem.
Narrowing the Field Further: Regular Primes
Gabriel Lamé, who worked on the proof for certain specific cases of n, also helped further the journey towards a general proof. He attempted a solution that involved complex numbers, by which he thought a general proof could be obtained. While this did not work, it set Ernest Krummer, another mathematician, thinking along the lines of his approach.
Krummer proceeded to try and prove a general case, using Lamé’s approach. The result was that he managed to prove the theorem for all n which are regular primes, a special category of prime numbers.
Later, in the 20th century, his idea was extended to irregular primes (those primes which are not regular), and proved with the help of computers for all primes upto 125000, and later all primes under 4,000,000 in 1993.
Unravelling the Mystery
So far, the computer based methods had proved Fermat’s Conjecture for all numbers under 4,000,000. Again, however, for it to be valid, it had to proved for all numbers.
So far, there was no large unifying approach to prove the Conjecture for all numbers. The best that mathematicians had so far done was to prove it for all regular primes, and all primes under 4,000,000.
The bold shot at a general solution came in 1955, in a seemingly unrelated field – elliptic curves.
Two Japanese mathematicians working in that field, Goro Shimura and Yutaka Taniyama, made a prediction that all elliptic curves were modular, that is, they could be associated with something that mathematicians call “modular forms“. This was still a conjecture, called Taniyama-Shimura-Weil Conjecture, after the three mathematicians who initially supported it.
Now, how does this relate to Fermat’s Conjecture? Gerhard Frey established the link in 1984. He suggested that if Fermat’s Conjecture was false, there would be a way of generating an elliptic curve that was not modular. This would counter the Taniyama-Shimura-Weil Conjecture. ****
His suggestion was later proved by Ken Ribet in 1986. This now meant that mathematicians had two ways to attack Fermat’s Theorem. They could either directly prove that it was true, or they could show that the Taniyama-Shimura-Weil was true. This would directly show that Fermat’s Conjecture was true.
So, Fermat’s Conjecture and the Taniyama-Shimura-Weil Conjecture were connected. If one was true, so was the other. If one was false, the same went for the other.
Andrew Wiles’ Journey to the Solution
Inspired by Ribet’s work and driven by a childhood fascination with Fermat’s Conjecture, British mathematician Andrew Wiles set off to work on the proof for it, in the indirect method.
He spent six years, between 1986 and 1993, working on the Taniyama-Shimura-Weil Conjecture, trying to prove it. He did his work in total secrecy, not letting anyone except his wife know he was working on it.
After several false starts and dead ends, he arrived at what he believed was the complete proof, in 1993. This very proof he presented in June 1993, in a series of lectures at Isaac Newton Institute of Mathematical Sciences.
While the proof caused widespread amazement and wonder in the world of mathematics, it emerged two months later that there was a problem in the proof that made it incomplete. Wiles had to return to his work, in hope of rectifying the error as soon as possible.
As time passed on, pressure rose from the mathematical community to publicize his partial proof, which might lead other mathematicians to the solution. However, Wiles refused, as he felt he deserved a chance to finish what he started.

Almost at a dead end, he turned to the help of one of his former students, Richard Taylor, to finish the matter.
On 19 September 1994, close to giving up the proof, he suddenly had an epiphany about his approach to the proof. This helped him close up the gaps in his logic for the proof, and present a final complete form of the Conjecture. Fermat’s Conjecture had at last become Fermat’s Last Theorem.
The proof was published in the May 1995 edition of the Annals of Mathematics and was hailed as an epic achievement. Indeed, it was the end of a journey that started 358 years ago.
What Does This Mean for Mathematics?
Fermat’s Last Theorem doesn’t have any direct applications in mathematics or any other field for that matter. Yet, it is cherished as a mystery that captured the imagination of innumerable numbers of mathematicians in the 358 years it took to prove it. Its proof is special not for its usefulness, but its beauty.
That said, the work that went into proving Fermat’s Last Theorem enriched mathematics a lot. Even the failed attempts helped set mathematicians along the right track and provided the knowledge they did not have.
The mathematical leaps made along the way gave a lot to other fields of mathematics too. For example, Ernest Kromer’s work in the mid 19th century helped generate the idea of ideal numbers. Similarly, Sophie Germain’s work had important consequences for number theory.
Even more spectacularly, the path to proving Fermat’s Last Theorem led to the proof of the Taniyama-Shimura-Weil Conjecture.
Taniyama-Shimura-Weil Conjecture is now knows as Modularity Theorem and have important applications in the field of elliptic curves.
All said and done, Fermat’s Last Theorem inspired generations of mathematicians to pursue what seemed to be an unattainable goal, and arrive at diverse results along the process. Its story remains an inspiration for other mathematicians pursuing the other unsolved mysteries of mathematics.
FAQ
Yes, Fermat’s last theorem was proved in 1995 by Andrew Wiles. He published his general proof in May 1995 edition of the Annals of Mathematics.
Fermat’s Last Theorem doesn’t have any direct applications in mathematics or any other field for that matter. But the work which went into the proof of the theorem enriched mathematics a lot.

