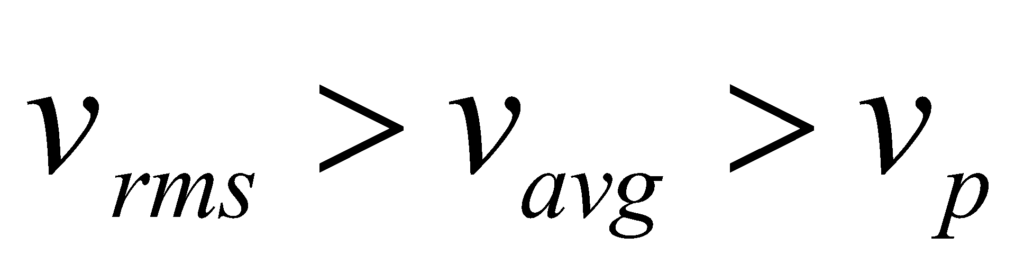The Maxwell-Boltzmann distribution is a type of probability distribution named after James Clark Maxwell and Ludwig Boltzmann. It is an integral part of statistical mechanics.
The distribution was first proposed by the Scottish physicist Maxwell in 1859 to describe the distribution of velocities among the molecules in a gas.
Later, in 1871, the German physicist Boltzmann generalised Maxwell’s calculations to describe the distribution of energies in a molecule.
Index
Derivation of the Distribution
Consider a system of particles, where the particles are identical but are indistinguishable. For the total number of particles being n, the fixed volume of the system being V and the system’s fixed energy being U, we have to identify the fraction of particles present at a given energy level.
The energy levels of the system are fixed. Let the energy levels of the system be ε0, ε2, ……, εr.
The number of particles in each energy level can be represented by n0, n1, ……., nr.
To move ahead, we need to define a microstate.
In physics, a microstate is defined as the arrangement of each molecule in the system at a given instant. For each macroscopic property of the system (macrostate), there exist many microstates that make up the macrostate.
The number of ways to attain a given microstate is given by the formula,
ω= n! / n0!n1!…nr!
We need to know the values of ni that can maximise the value of ω. To maximise this value, we obtain the value of ln(ω).
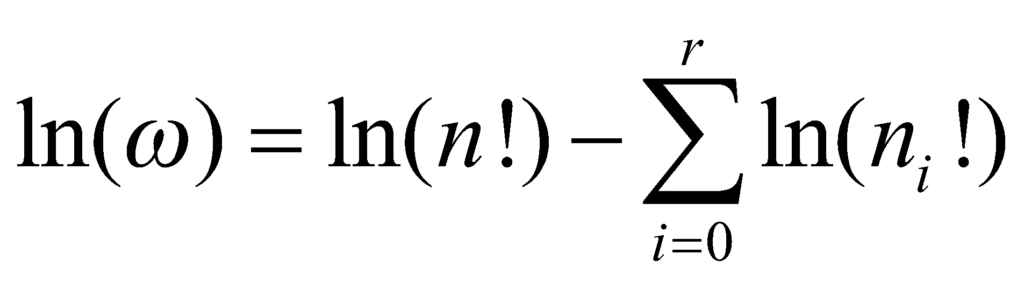
According to Sterling’s approximation,
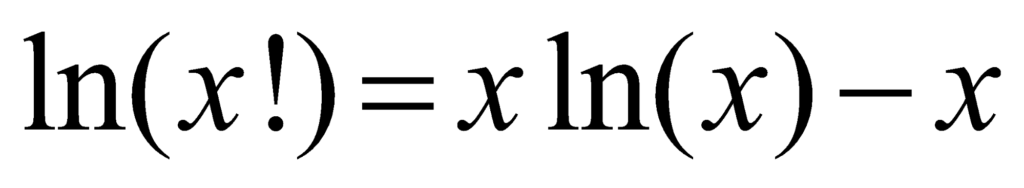
Thus:
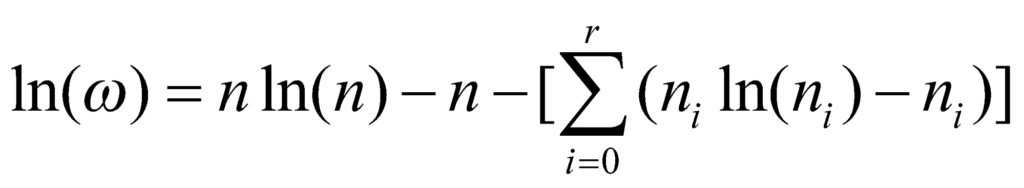
Now, we take the derivative of the above relation to obtain:
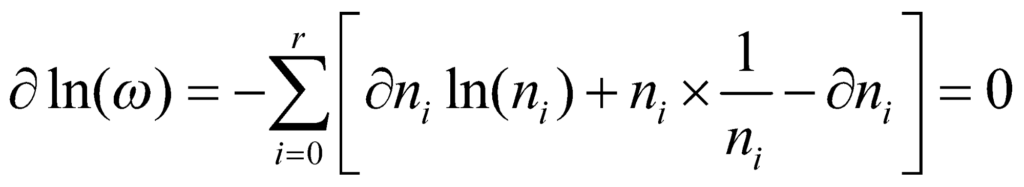
Therefore, the sum of all the changes in the system must add up to zero. From this, we can infer that:
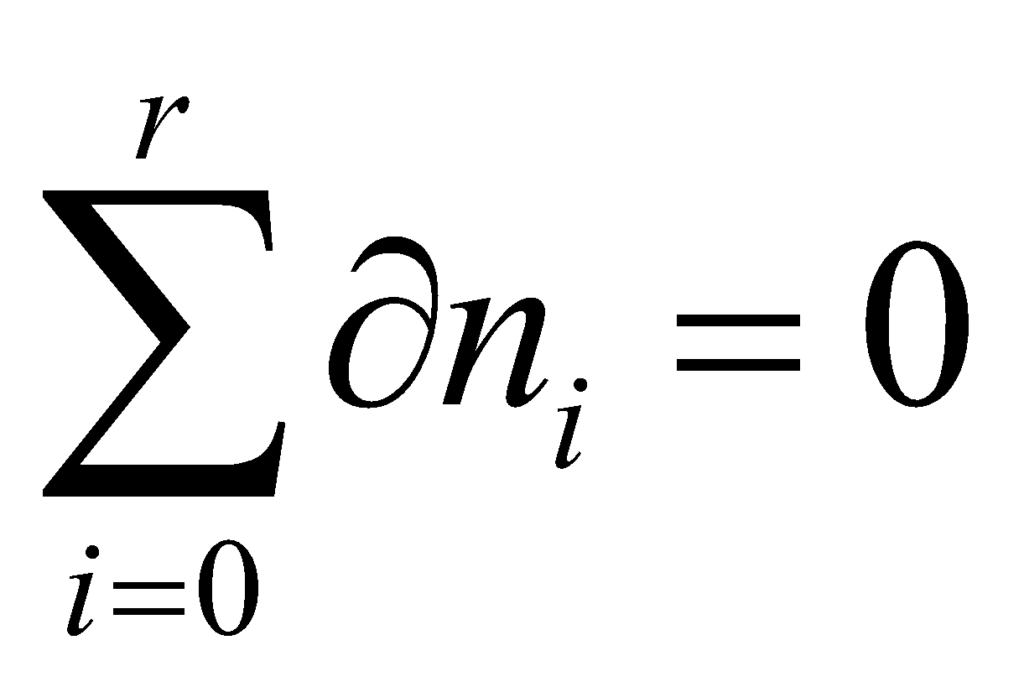
The total energy of the system must be constant. Thus:
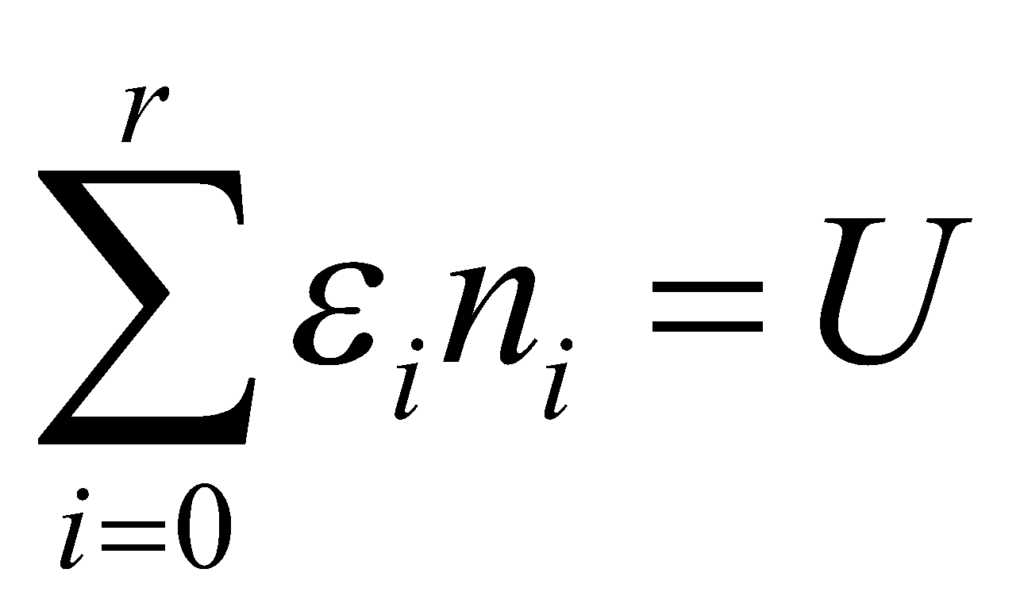
where U is a constant. Thus, on differentiating:
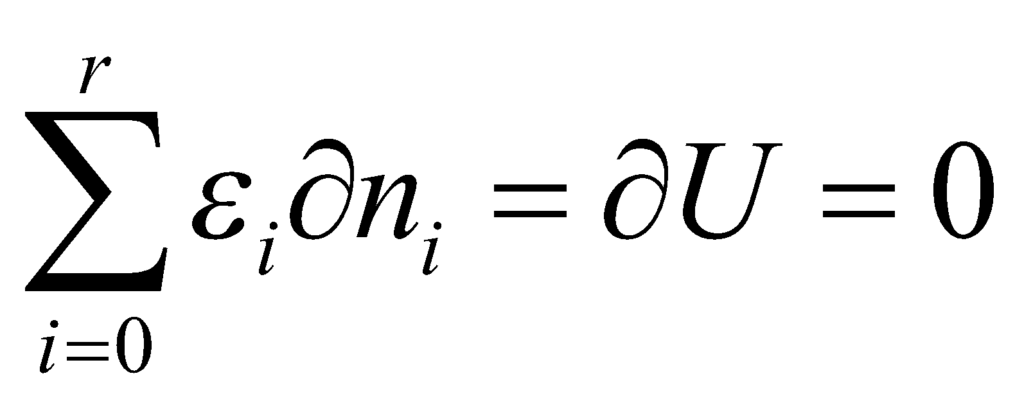
Using Lagrange’s method of undefined multipliers, we obtain the following relation:
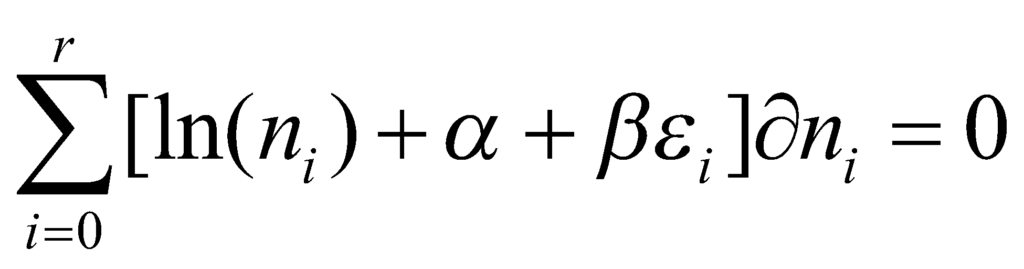
For the above relation to be true, the following must hold:
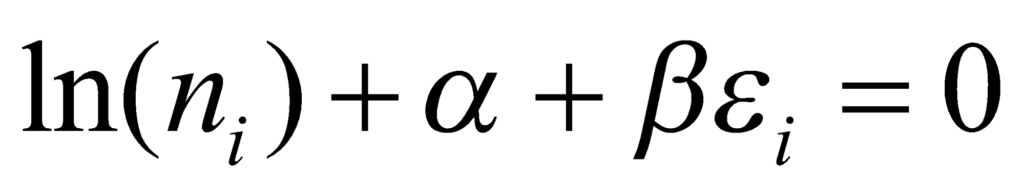
Simplifying the above relation, we get:
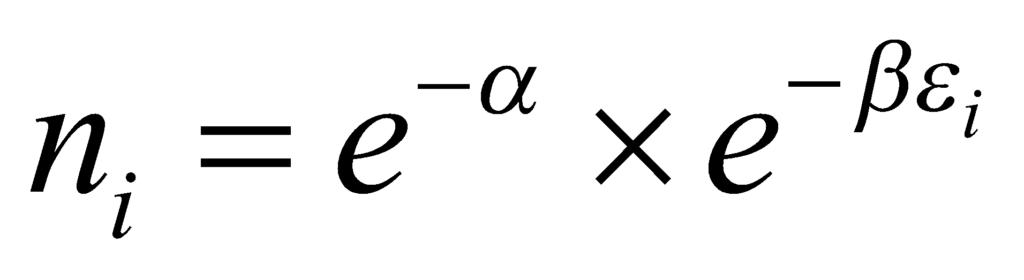
The above equation describes the number of particles in the ith level. Taking the sum of the equation over i, the only parameter that is a variable is εi. We obtain:
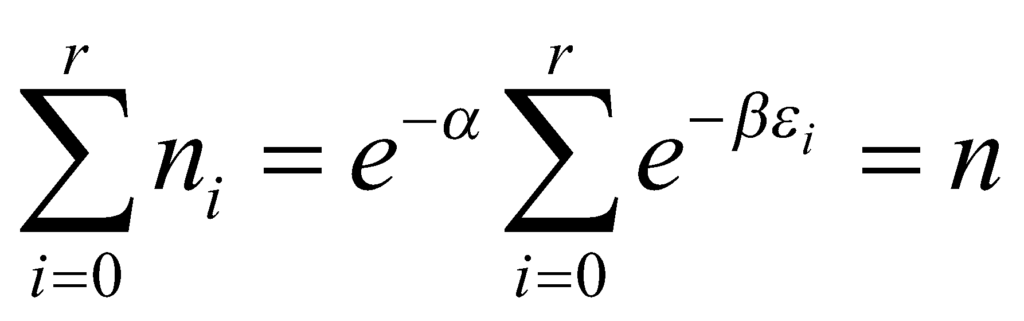
Here, we define the partition function P such that:
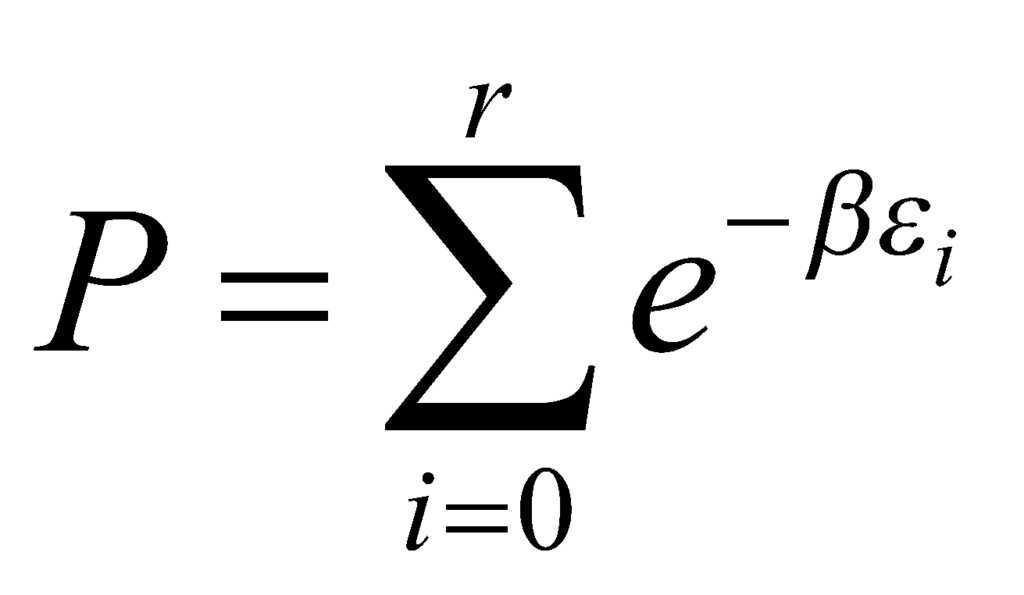
Substituting the partition function in the above equation, we get the following:
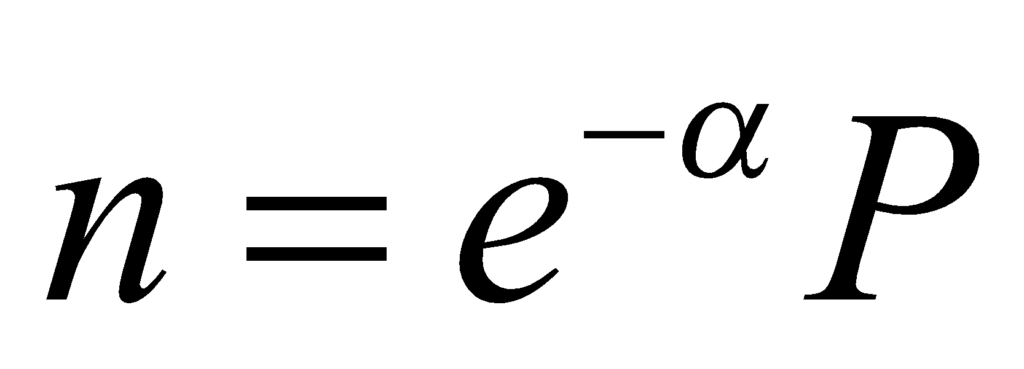
Thus, the number of particles in the ith level becomes:
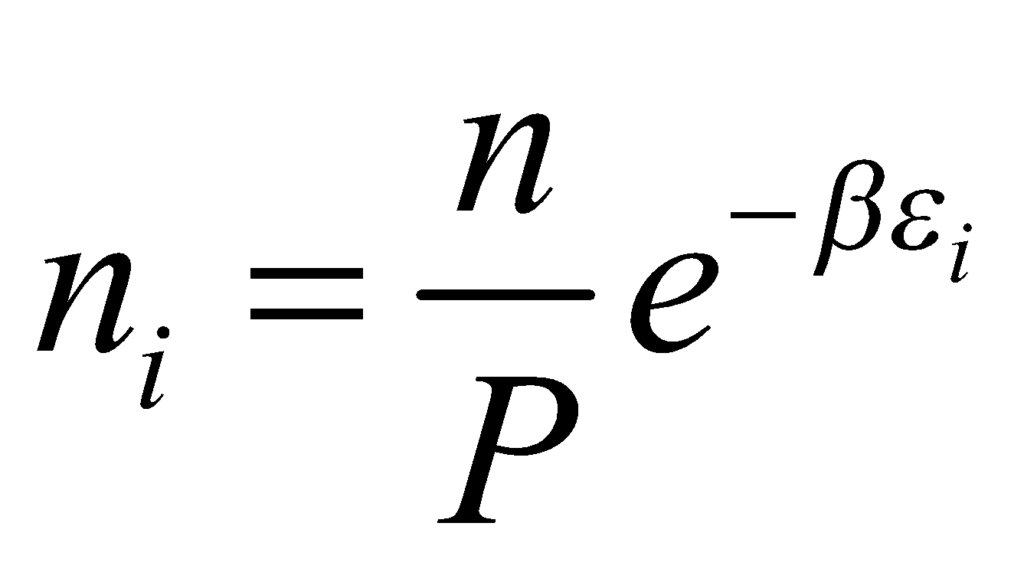
The value of β in the above equation is β = 1/(kBT), where kB is the Boltzmann constant and T is the temperature of the system. Substituting the value of in the equation, we obtain:
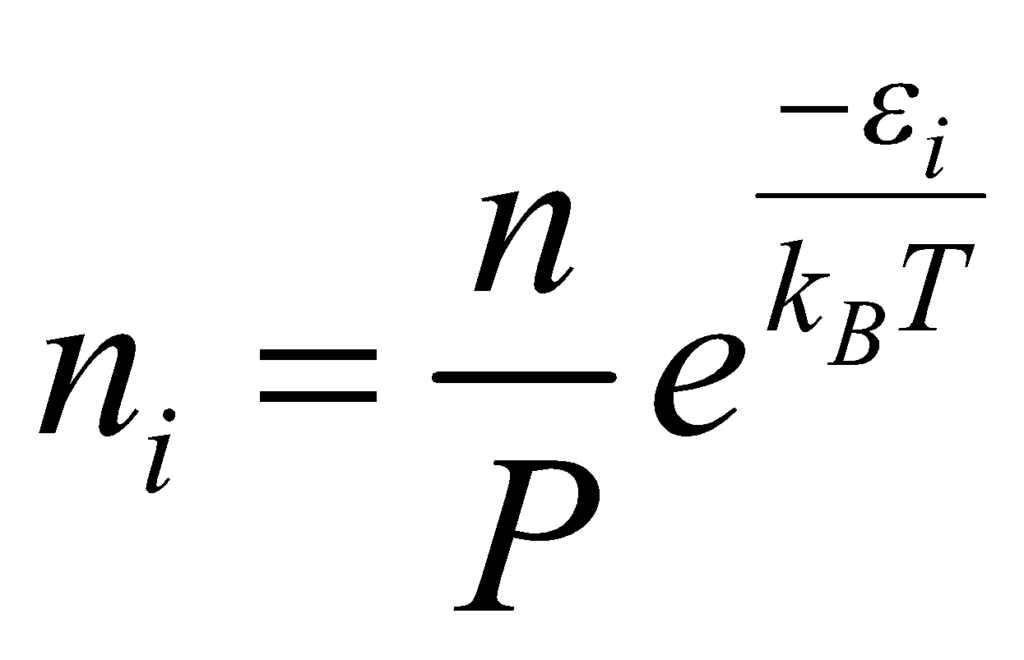
The above relation describes the number of particles in the most probable microstates and is known as the Maxwell Boltzmann Statistics Expression.
Take the potential energy to be zero. Thus the only contribution to the total energy U comes from the kinetic energy E. The relationship between kinetic energy and momentum is given by:
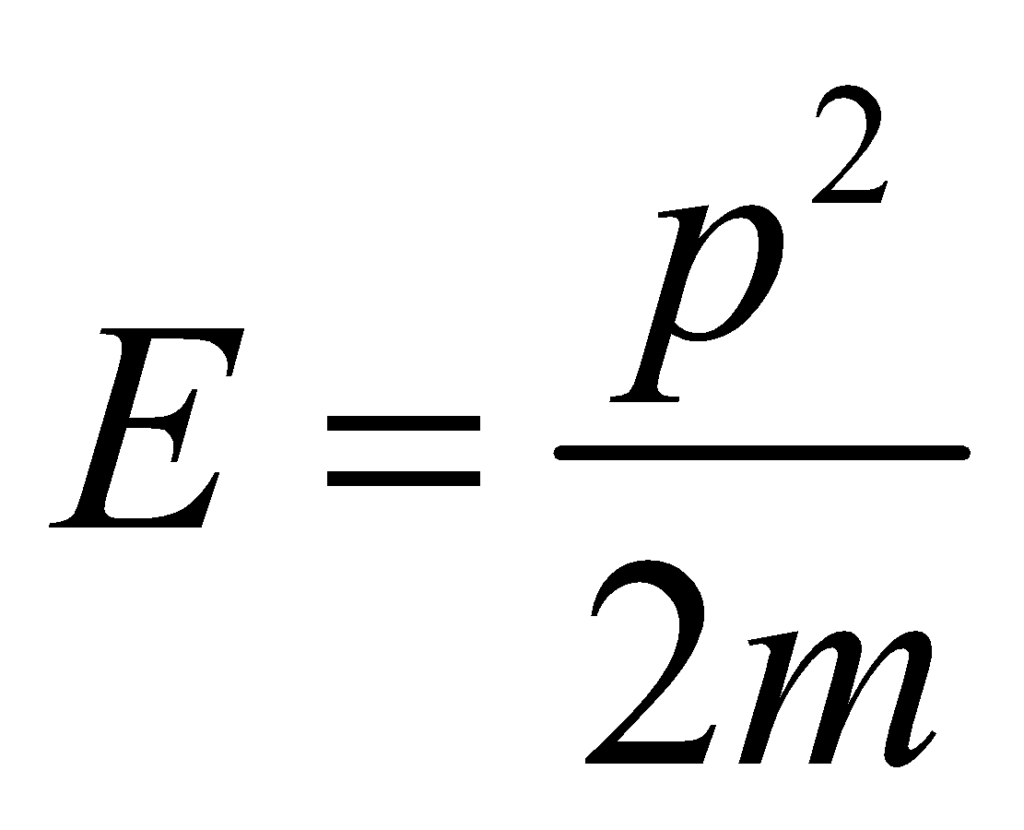
where p2 is the square of the momentum vector p = [px, py, pz]. Thus, the Maxwell Boltzmann Statistics Expression can be rewritten as:
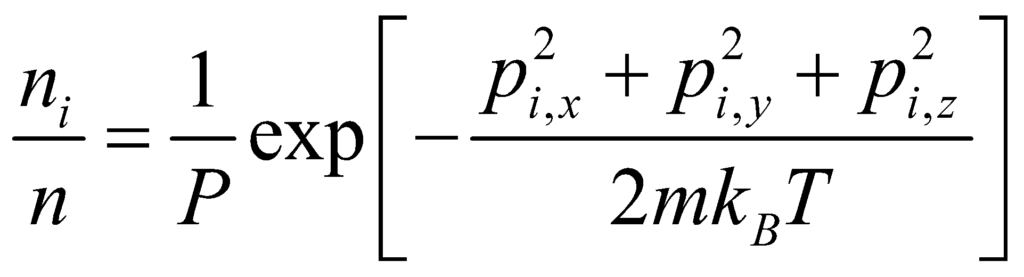
Here, m is the molecular mass of the gas, and T is the thermodynamic temperature (in Kelvin). The distribution of ni:n is proportional to the probability density function fp for finding a molecule with the given momentum components. Thus:
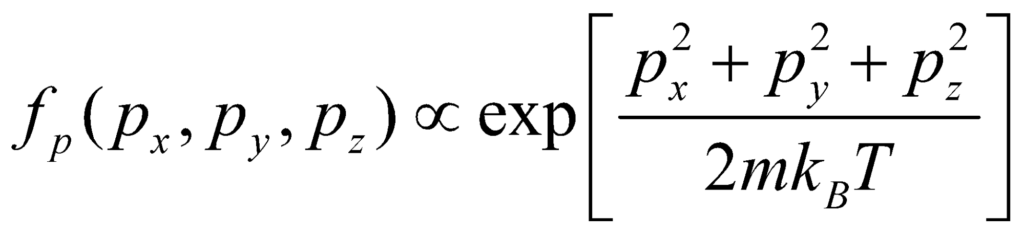
The normalising constant can be determined through understanding that the probability of a molecule having some momentum must be the Maxwell Boltzmann Statistics relation. Integrating the above relation over all px, py and pz yields a factor of:
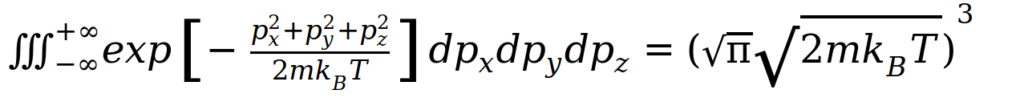
Thus, the normalised function becomes:
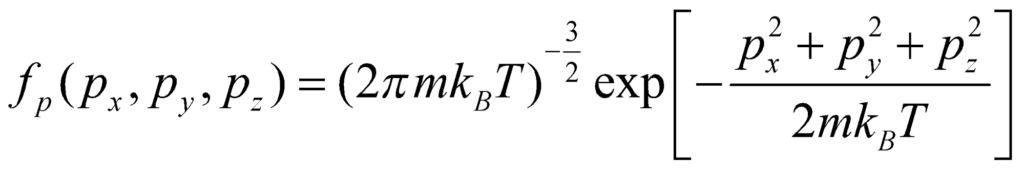
From this equation, we can find the energy distribution by substituting the relation between E and p, and then integrating, to obtain:
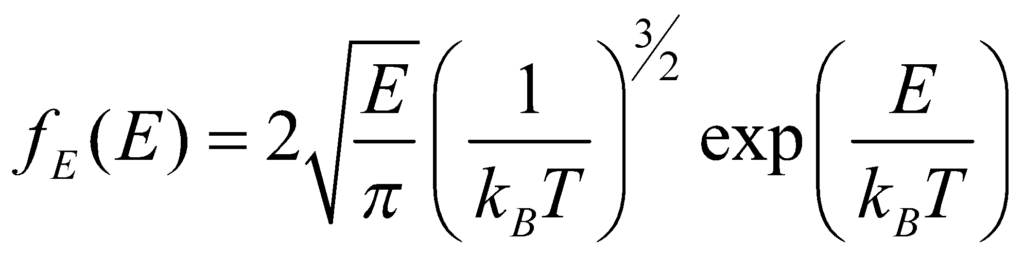
And the velocity vector distribution can be derived by identifying that the velocity probability density fv is related to the momentum probability distribution by:
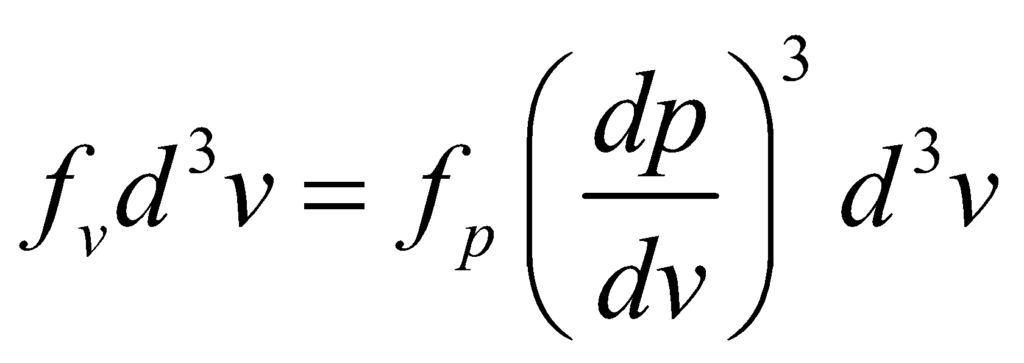
Using p = mv, we get:
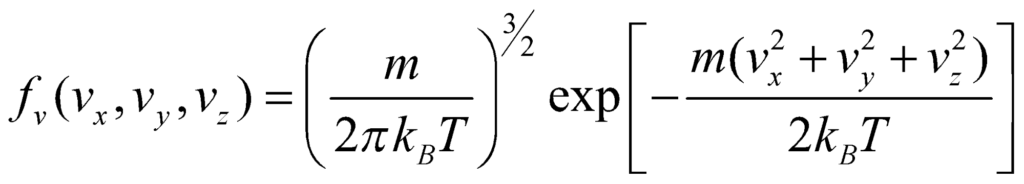
This is the Maxwell Boltzmann Velocity Distribution function. For the distribution for speed, we obtain speed from the velocity components by:
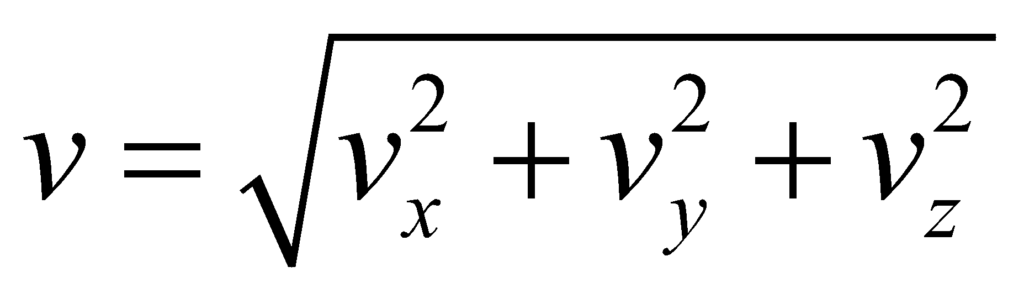
and the volume elements in the spherical coordinates is given by:
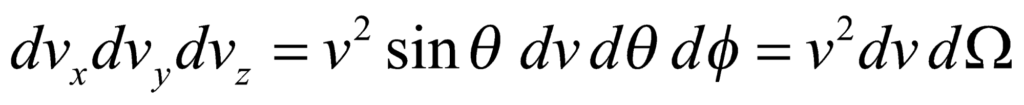
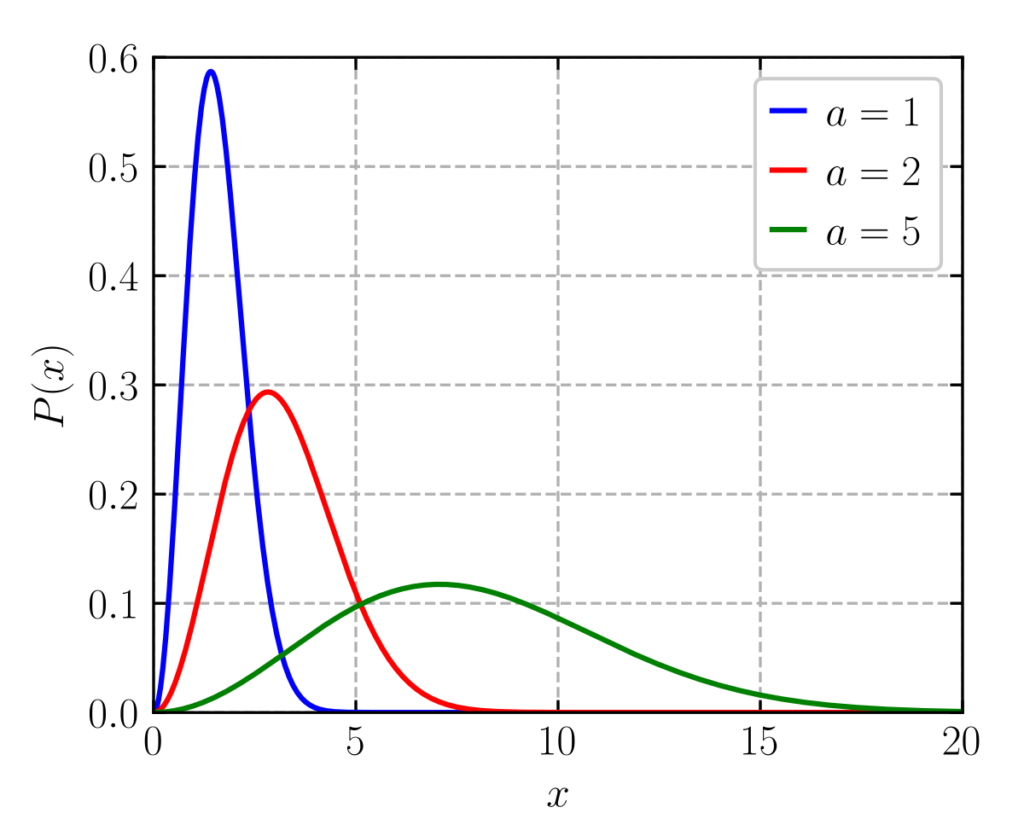
Integration over the solid angle gives an additional factor of 4π. Thus, the speed distribution is obtained as:
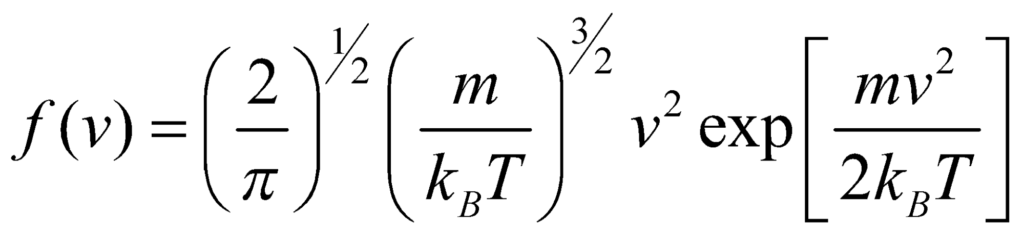
Typical Speeds
From the properties of Maxwell Distribution, we obtain three speed functions:
- The mean speed <v>, or vavg,
- The most probable speed (mode) vp,
- The root mean squared speed 〈√v2〉
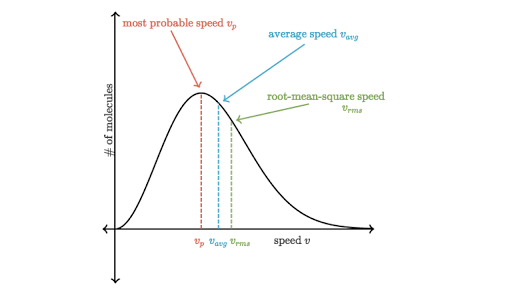
The Most Probable Speed (vp)
This is the speed most likely to be possessed by any molecule of the same mass m in the system. It corresponds to the peak (also called mode) of the distribution function.
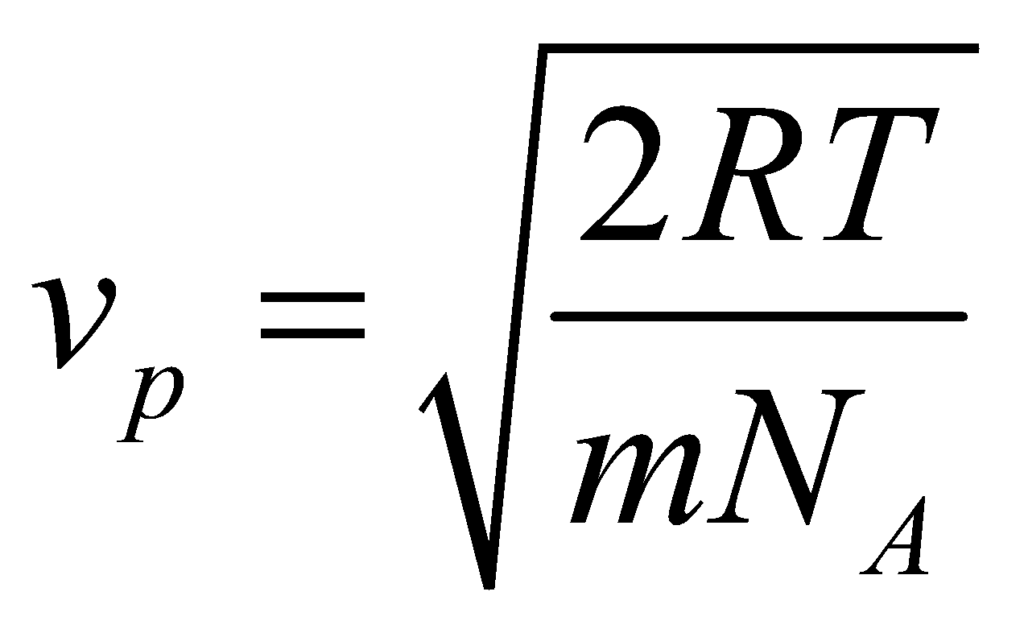
The Average Speed (Vavg)
The average speed is the average of all the speeds of all the molecules. It is the expected value of the speed distribution.
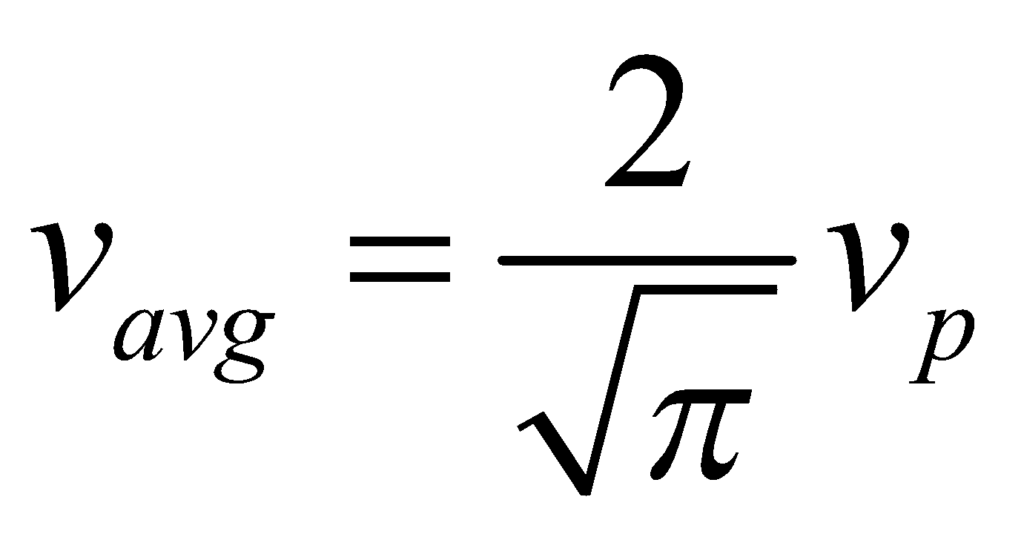
Root Mean Square Velocity (vrms)
The root mean square speed vrms is the square root of the mean square speed, corresponding to the speed of a particle with median kinetic energy.
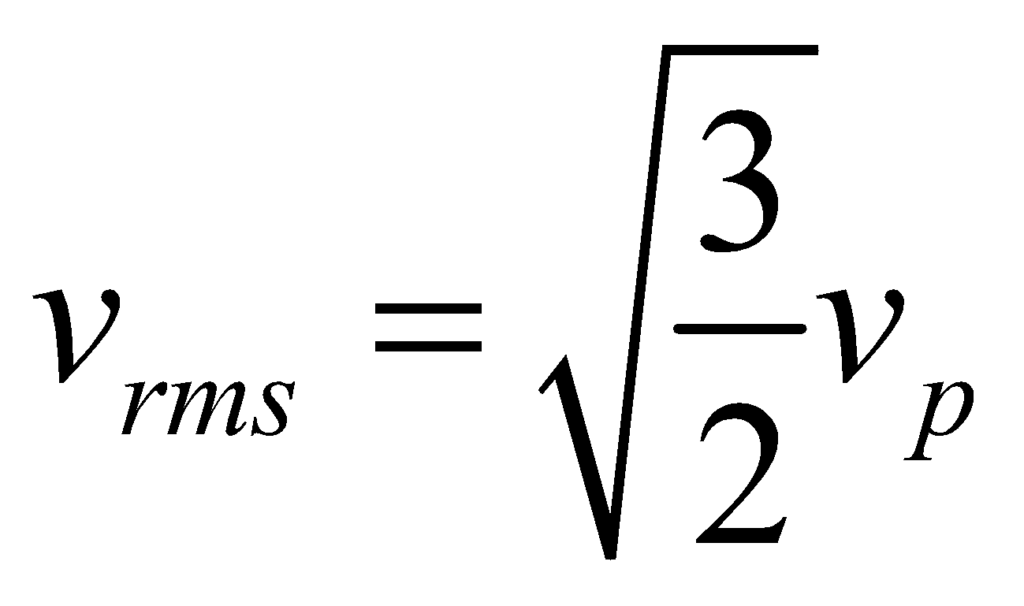
Thus, we can see that: