The Nernst Equation is used to find the potential of an electrochemical cell or an oxidation/ reduction reaction under conditions of changing temperature and concentration of the electrolyte. It arises from a need to measure the potential of electrochemical cells so as to determine the voltage of a cell.
Electrochemical cells form a large part of our lives. Various types of batteries are present everywhere from our phones to our cars. It is crucial to understand these cells, so as to make more efficient and advanced batteries.
Index
Electrochemical Cell
An electrochemical cell uses a spontaneous redox reaction which undergoes indirectly, to produce electrical energy. An electrochemical cell basically converts chemical energy into electrical energy. Spontaneous redox reactions proceed with a decrease in free energy (G), which is converted to electrical energy in an electrochemical cell, producing a current.
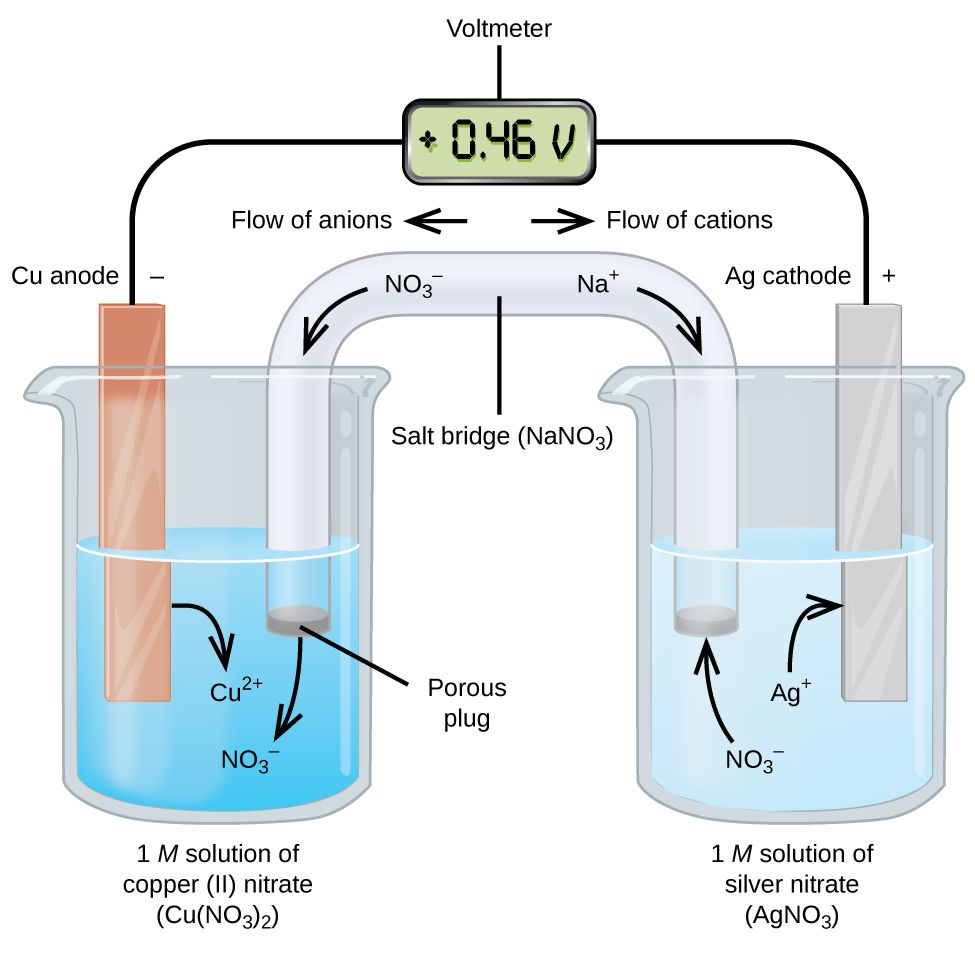
The way the electrochemical cell makes the redox reaction ‘indirect’ is by splitting the reaction into an oxidation component and a reduction component. The reactions are known as half cell reactions, with the anode being the site of oxidation half cell reaction and the cathode being the reduction half cell reaction (refer image above).
Measuring Potential of the Half Cell Reactions
While measuring potentials of half cell reactions we are faced with a unique problem. No reduction or oxidation reaction occurs on its own. There will always be an oxidation or reduction reaction coupled with it respectively. To solve this problem we measure the potential of half cell reactions against a reference electrode, whose reduction and oxidation potential we assume to be zero.
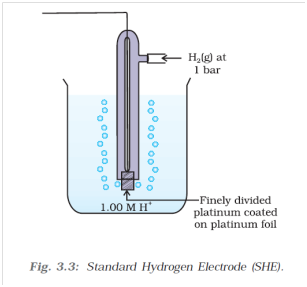
For this we take the standard hydrogen electrode. It consists of H2 gas at 1 bar pressure, as well as a 1M H+ ion concentration, which is from an acid (like, HCl for example). The system is at a temperature of 298K. The H2 gas can oxidise to yield H+ ions, or the H+ ions can reduce to produce H2 gas. This oxidation and reduction reaction can be coupled with a half cell reaction, and the resultant potential of the cell is assigned to the half cell reaction. The potential measured is known as the standard electrode potential as is denoted as Eo.
This means that the potential of the cell (Ecell) can be calculated as:-
Eocell = Eooxidation half reaction at anode + Eoreduction half reaction at cathode
The Nernst Equation Introduced
But what is the potential if the conditions are not ‘standard’. To solve this problem we use the Nernst Equation, which accounts for changes in the concentration and temperature. The equation is –
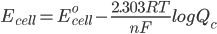
where,
Ecell is the potential of the cell
Eocell is the standard potential of the cell
R is the gas constant
n is the number of electrons transferred in the cell reaction
F is Faraday’s constant, which is the charge on one mole of electrons and has the value, 1F = 96500 C/mol
Qc is the reaction quotient
Reaction Quotient is a fraction, where the numerator is a product of reaction product concentrations each raised to the power of its stoichiometric coefficient, and the denominator is a similar product of reactant concentrations raised to their stoichiometric coefficient.
For the reaction :- aA +bB → cC + dD
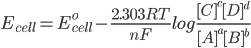
where, [x] is the concentration of x
If we input the values –
R = 8.314 J/K-mol
T = 298 K
F = 96500 C/mol
The equation reduces to –
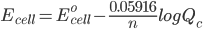
Applications of the Nernst Equation
The Nernst equation’s applications lie in the field of theoretical prediction of the potential of the cell when the conditions are not standard. They can be elucidated as –
1) Standard Hydrogen Electrodes have their own share of problems. It is difficult to maintain the concentration of H+ ions at 1M, as well have the gases at a pressure of 1 atm. At changed concentrations, it becomes difficult to measure the values of the potential of the cell. Inputting the new concentrations of the reactants and products in the reaction quotient term of the Nernst Equation helps us to accommodate these changes in concentration.
2) The temperature while measuring at standard concentrations is 298K or 25oC. The temperature of the electrochemical cell might not necessarily be at 298K. How do we account for changes in potential with temperature? The Nernst Equation helps to deal with temperature changes, and figure out theoretically how the potential of a cell changes.
3) The Nernst Equation is not restricted to a cell!
The Nernst Equation is not restricted to a cell and can be extended to a half cell reaction. Here are some examples:-
1) For the half cell reaction :-
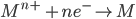
[e– is an electron]
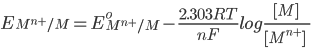
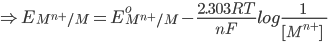
[Pure solids or liquids are removed from the reaction quotient, because their effective concentrations stay constant throughout the reaction]
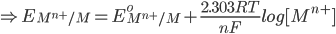
2) For the half cell reaction :-
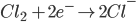
[e– is an electron]
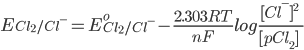
[While considering the concentrations of gases we take their partial pressures. Here pCl2 is the partial pressure of Cl2 and is representative of the concentration of the chlorine gas]

