Parallel axis theorem and Perpendicular axis theorem are two very important theorems in the field of rigid body mechanics.
They help us generalize results about moments of inertia of objects to a variety of situations. This helps us in many calculations that get simplified in the process.
Index
Moment of Inertia
Moment of inertia is the equivalent of mass in rotational dynamics. We know that it is relatively harder to move a heavier object than a lighter one. Similarly, it is harder to rotate an object with more moment of inertia than one with a lesser moment of inertia.
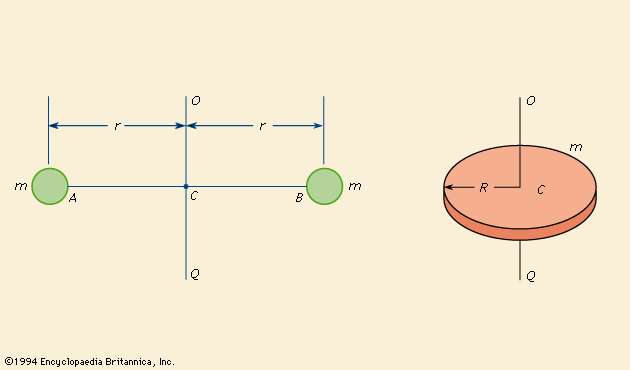
An interesting fact about the moment of inertia is that it depends not just on the object, but also the axis of rotation. The same object can have different moments of inertia depending on which axis we are rotating it about.
To visualize this, consider rotating a uniform rod. It is evidently easier to rotate the rod about its centre, than its ends. This has a direct relation to one of the theorems we will discuss here. Another example is the bicycle wheel. It is easier to rotate it about the centre than the rim.
In mathematical language, moment of inertia is defined as follows:
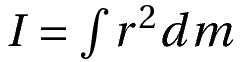
Where
r refers to the distances from the axis of rotation
dm is the elementary mass
I is the moment of inertia
Parallel Axis Theorem
Parallel axis theorem states the following:
Let the moment of inertia about the centre of mass be I. The moment of inertia about another axis parallel to this axis is simply the sum of I and md2, where d is the distance between the axes and m is the mass of the object.
Mathematically, the parallel axis theorem formula is,
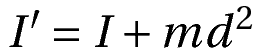
where
d is the perpendicular distance between the axes.
m is the mass of the object
I is the moment of inertia about the centre of mass
I’ is the moment of inertia about the new axis
This can be proved rigorously by calculating the terms for I and I’ from the integral above.
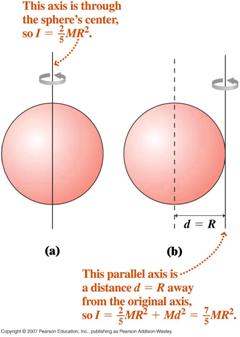
Let us take a rod as an example to demonstrate parallel axis theorem. Assume the mass of the rod to be M and length to be L.
The moment of inertia about a perpendicular axis through the centre of mass is (1/12)ML2. So, if we consider rotating it around a parallel axis at the end,
d = L/2 (the distance between the centre and the end)
I’ = I + md2 (from parallel axis theorem and I’ is the moment of inertia at end)
Putting I, m, d values into above equation
we get, I’ = (1/12)ML2 + M(L/2)2
=> I’ = (1/12)ML2 + (1/4)ML2
=> I’ = (1/3)ML2
This is a clear application of the parallel axis theorem that demonstrates its usefulness.
Perpendicular Axis Theorem
This is applicable only to planar objects, unlike parallel axis theorem. This means it can be used for objects like discs and rings, as well as sheets.
The statement of the theorem is as follows:
Let the moment of inertia about an axis perpendicular to the planar surface be Iz, and Ix and Iy be the moments of inertia about two mutually perpendicular axes in the plane. The two axes should intersect where the first axis cuts the plane. Then, we write the perpendicular axis theorem formula as:
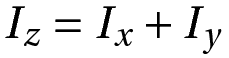
This theorem can be extremely useful when we know two moments of inertia of a planar object and want to know the third, provided they all are perpendicular.
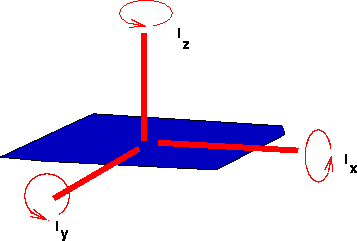
An example of perpendicular axis theorem in action is when we consider a ring of mass M and radius R.
About an axis perpendicular to the ring and passing through its centre, it has a moment of inertia MR2.
Now imagine rotating it about axes through the centre but in the plane. We can make use of symmetry here.
We can see that any such two perpendicular axes have the same moment of inertia, say Ix.
Thus, clearly, by the theorem,
2Ix = MR2
Ix = 0.5MR2
Applications
Together, perpendicular axis theorem and parallel axis theorem can be used to simplify the calculations of moment of inertia.
They can help us extend our knowledge of the moment of inertia from one axis to other related axes. Thus, we will find it easier to study the rotational dynamics of rigid bodies in various conditions.
FAQ
Parallel axis theorem can be used for finding the moment of inertia of a rigid body whose axis is parallel to the axis of the known moment and it is through the center of gravity of the object.
The radius of gyration is defined as the distance of a point where the whole area of the body is assumed to be concentrated from the given axis.

