The Pythagorean Theorem, also called the Pythagoras Theorem, is a fundamental relationship in Euclidian Geometry. It relates the three sides of a right-angled triangle.
The theorem states that the square of the side that is the hypotenuse (the side opposite to the right angle) is the sum of the square of the other two sides.
Mathematically, for a right triangle shown below,
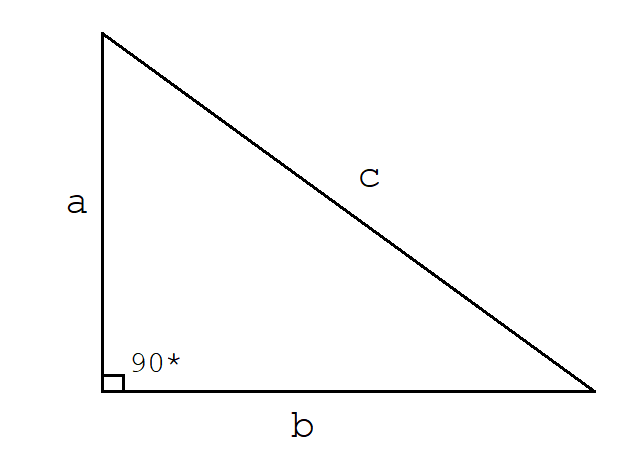
the Pythagorean Theorem is expressed as
a2 + b2 = c2 (Pythagoras Equation)
The exact date of the development of the Pythagoras Theorem is not known. There is some evidence of it being used as early as the age of the Mesopotamian civilization which is a 1000 years ago Pythagoras was born.
This theorem was proved multiple times by various methods, including algebraic and geometric methods. Let us look at various methods of proving the Pythagorean theorem.
Index
Methods of Proofs of the Pythagorean Theorem
Proof by rearrangement
Consider the figure, as shown below:
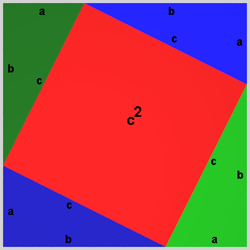
Here, we see that the red square in the centre has an area of c2. The overall larger square consists of right-angled triangles of sides a + b, with the centre red square. Now, rearrange the system as shown:
As seen here, when rearrangement is done, the red area that was c2 is now evenly split between a2 and b2. From this, we see that a2 + b2 = c2. Thus, the Pythagorean theorem is proved.
Proof Using Similar Triangles
Consider two triangles as shown:
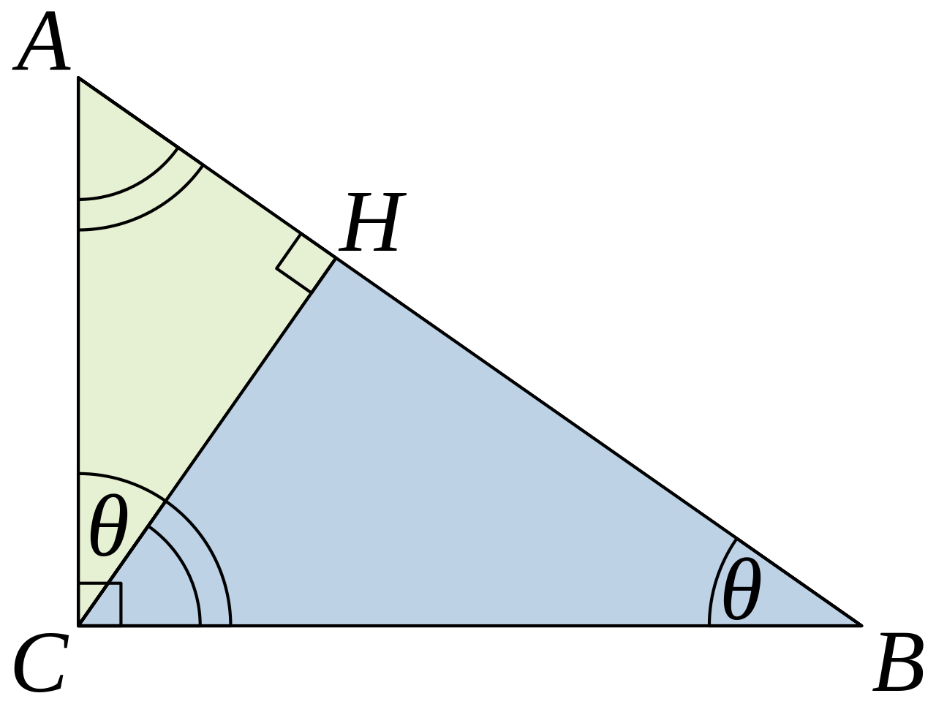
This proof is based on the sides of two similar triangles’ proportionality: the ratio of any two corresponding sides of similar triangles is the same regardless of the triangles’ size.
Let ABC represent a right triangle, with the right angle located at C, as shown on the figure. Draw the altitude from point C, and call H its intersection with the side AB. Point H divides the length of the hypotenuse c into parts d and e.
The new triangle ACH is similar to triangle ABC, because they both have a right angle (by definition of the altitude), and they share the angle at A, meaning that the third angle will be the same in both triangles as well, marked as θ in the figure. By similar reasoning, the triangle CBH is also similar to ABC. The triangles’ similarity requires the triangle postulate: The sum of the angles in a triangle is two right angles.
By the similarity of right triangles, we have the following relation:
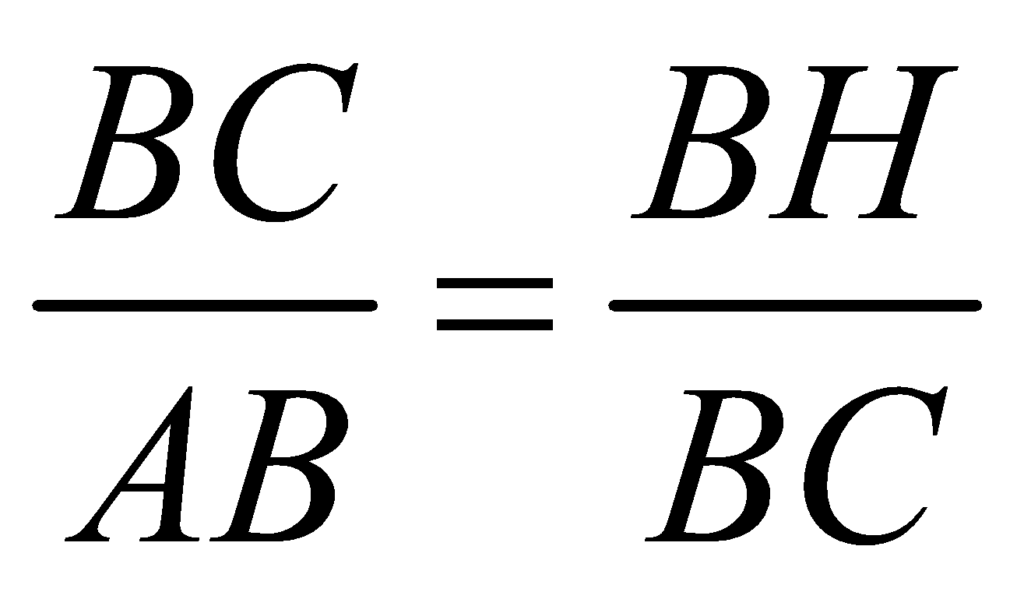
and
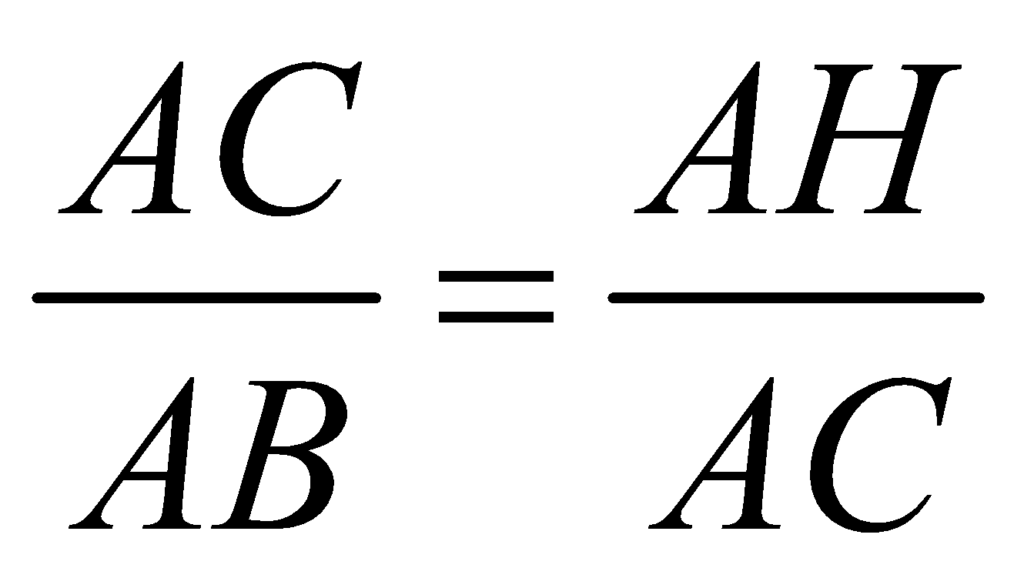
Cross multiplying, we obtain the relations:
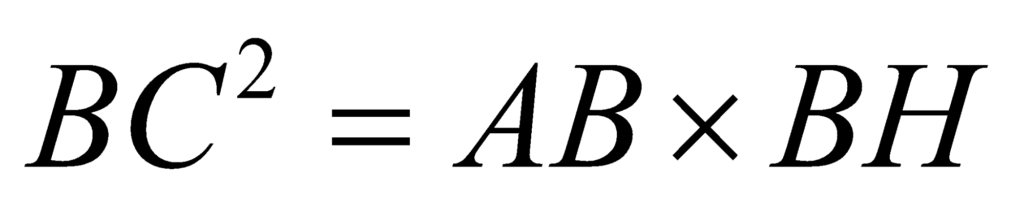
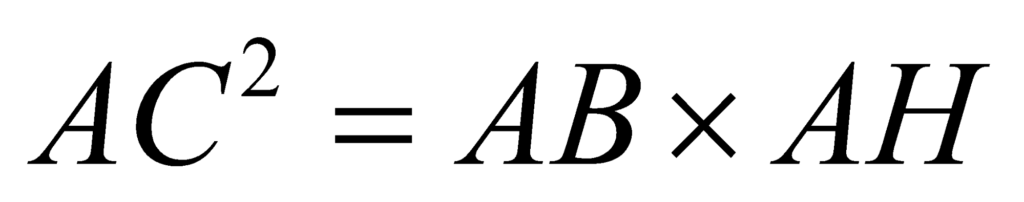
Adding the two relations that we have, we obtain:
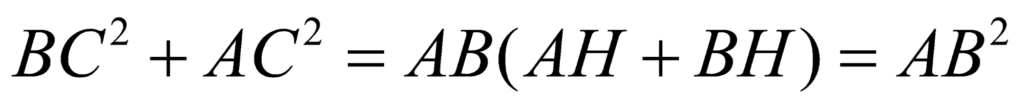
Hence proved.
Euclid’s Proof
Euclid gave this proof in his work, “Elements“. Consider the diagram below:
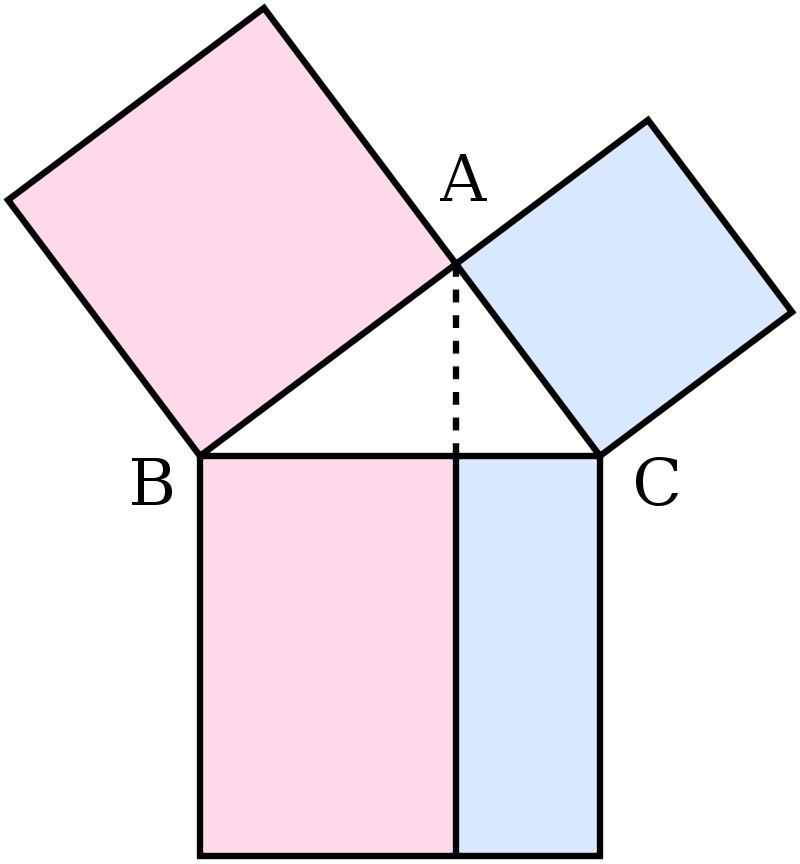
Let A, B, C be the right triangle’s vertices, with a right angle at A. Drop a perpendicular from A to the side opposite the hypotenuse in the square on the hypotenuse. That line divides the square on the hypotenuse into two rectangles, each having the same area as one of the two squares on the legs.
For the formal proof, we require four elementary lemmas which are as follows:
- If two triangles have two sides of the one equal to two sides of the other, each to each, and the angles included by those sides equal, then the triangles are congruent (side-angle-side).
- A triangle’s area is half the area of any parallelogram on the same base and having the same altitude.
- The area of a rectangle is equal to the product of two adjacent sides.
- The area of a square is equal to the product of two of its sides (follows from 3).
Next, each top square is related to a triangle congruent with another triangle related to one of two rectangles making up the lower square.
The proof is as follows:
- Let ACB be a right-angled triangle with right angle CAB.
- Squares CBDE, BAGF, and ACIH, are drawn on each of the sides BC, AB, and CA, respectively. The construction of squares requires the immediately preceding theorems in Euclid and depends upon the parallel postulate.
- From A, draw a line parallel to BD and CE. It will perpendicularly intersect BC and DE at K and L, respectively.
- Join CF and AD, to form the triangles BCF and BDA.
- Angles CAB and BAG are both right angles; therefore, C, A, and G are collinear. Similarly, for B, A, and H.
- Angles CBD and FBA are both right angles; therefore, angle ABD equals angle FBC, since both are the sum of a right angle and angle ABC.
- Since AB is equal to FB and BD is equal to BC, triangle ABD must be congruent to triangle FBC.
- Since A-K-L is a straight line, parallel to BD, then rectangle BDLK has twice the area of triangle ABD because they share the base BD and have the same altitude BK, i.e., a line normal to their common base, connecting the parallel lines BD and AL. (lemma 2)
- Since C is collinear with A and G, square BAGF must be twice in the area to triangle FBC.
- Therefore, rectangle BDLK must have the same area as square BAGF = AB2.
- Similarly, we can show that rectangle CKLE must have the same area as square ACIH = AC2.
- Adding these two results, AB2 + AC2 = BD × BK + KL × KC
- Since BD = KL, BD × BK + KL × KC = BD (BK + KC) = BD × BC
- Therefore, AB2 + AC2 = BC2, since CBDE is a square.
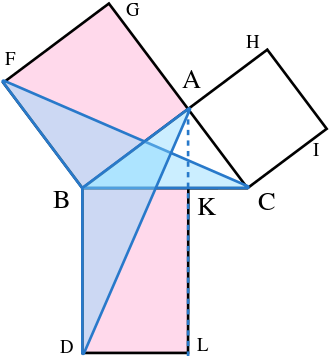
Hence proved.
Proof using Algebraic Methods
For algebraic methods, consider the following diagram:
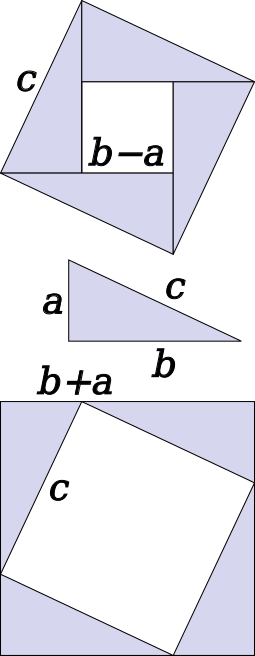
In the first diagram, the area of the square with side c, is given by:
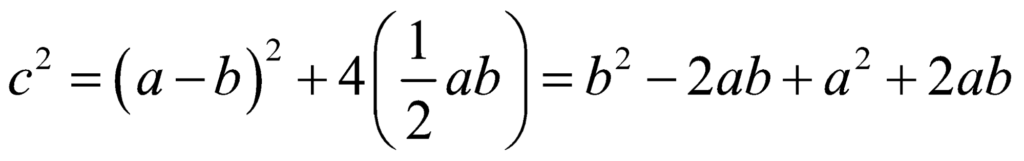
Thus, on simplifying, we obtain,
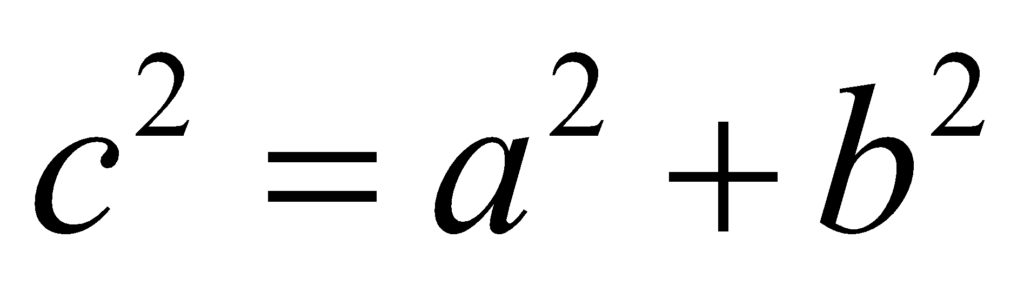
Applications
In daily mathematics, we obviously use the theorem for calculating hypotenuse of right angles triangle (Hypotenuse Calculator), for finding the diagonal of a square.
In our current lives, the theorem has a lot of applications in construction, woodworking and other practical aspects. Besides these, the theorem has had a significant impact on mathematics– for example, it helped the ancient Greeks prove the existence of irrational numbers.

