Quantum computers are computers which uses quantum phenomena such as entanglement and superposition to perform computing functions.
Where a traditional computer uses bits, which are strings of numbers (think of the binary system, with 0s and 1s), to store information, a quantum computer uses a qubit.
One can imagine a qubit like storing 0s and 1s in two distinguishable quantum states. To understand quantum computing, we first need to understand a couple of terms and definitions in quantum mechanics.
Index
Quantum Mechanical Background
Quantum
In physics and chemistry, the term quantum refers to the minimum amount of anything that can participate or is involved in an interaction.
We refer to physical quantities being “quantized”. This implies that physical properties can only take discrete values (like steps), and not continuous ones (like an analogue clock).
Superposition
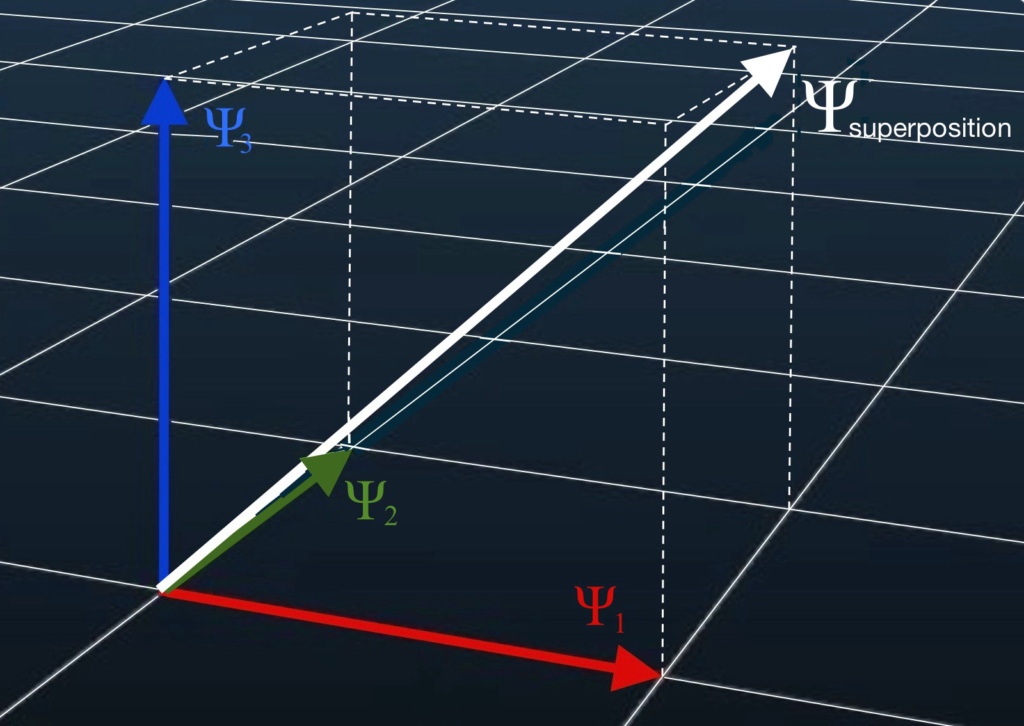
Quantum superposition within quantum mechanics is a fundamental principle that states that, like waves in classical physics, any two quantum states can be added together, or superposed.
A quantum state is a mathematical expression that describes the probability distribution for the outcomes of each possible measurement on a system.
The result of superposition will be a new valid quantum state, and every quantum state can be expressed as the result of the superposition of two or more distinct quantum states.
Entanglement
In the quantum model, entanglement is a physical phenomenon that occurs when a pair or group of particles are generated, interact or share special proximity in such a way that the quantum state of each particle of the pair or of the group cannot be described independently of the quantum state of the other particles, even when the particles are separated by a large distance.

How do Quantum Computers Work?
A quantum computer is a model of how to build a computer. The idea is that quantum computers can use certain phenomena from quantum mechanics, such as superposition and entanglement, to perform operations on data.
The basic principle behind quantum computation is that quantum properties can be used to represent data and perform operations on it. A theoretical model is the quantum Turing machine, also known as the universal quantum computer.
The idea of quantum computing is still very new. Experiments have been done. In these, a very small number of operations were done on qubits (quantum bit).
Both practical and theoretical research continues with interest, and many national governments and military funding agencies support quantum computing research to develop quantum computers for both civilian and military purposes, such as cryptanalysis.
Today’s computers, called “classical” computers, store information in binary; each bit is either on or off. Quantum computation use qubits, which, in addition to being possibly on or off, can be both on and off, which is a way of describing superposition, until a measurement is made. The state of a piece of data on a normal computer is known with certainty, but quantum computation uses probabilities. Only very simple quantum computers have been built, although larger designs have been invented.
If large-scale quantum computers can be built, they will be able to solve some problems much more quickly than any computer that exists today (such as Shor’s algorithm).
Quantum computers are different from other computers such as DNA computers and traditional computers based on transistors. Some computing architectures such as optical computers may use classical superposition of electromagnetic waves. Without quantum mechanical resources such as entanglement, people think that an exponential advantage over classical computers is not possible. Quantum computers cannot perform functions that are not theoretically computable by classical computers, in other words, they do not alter the Church-Turing thesis. They would, however, be able to do many things much more quickly and efficiently.
Quantum Information
Quantum information is the information of the state of a quantum system. It is the basic entity of study in quantum information theory and can be manipulated using quantum information processing techniques. It is an interdisciplinary field that involves quantum mechanics, computer science, information theory, philosophy and cryptography among other fields.
Qubits and Quantum Information
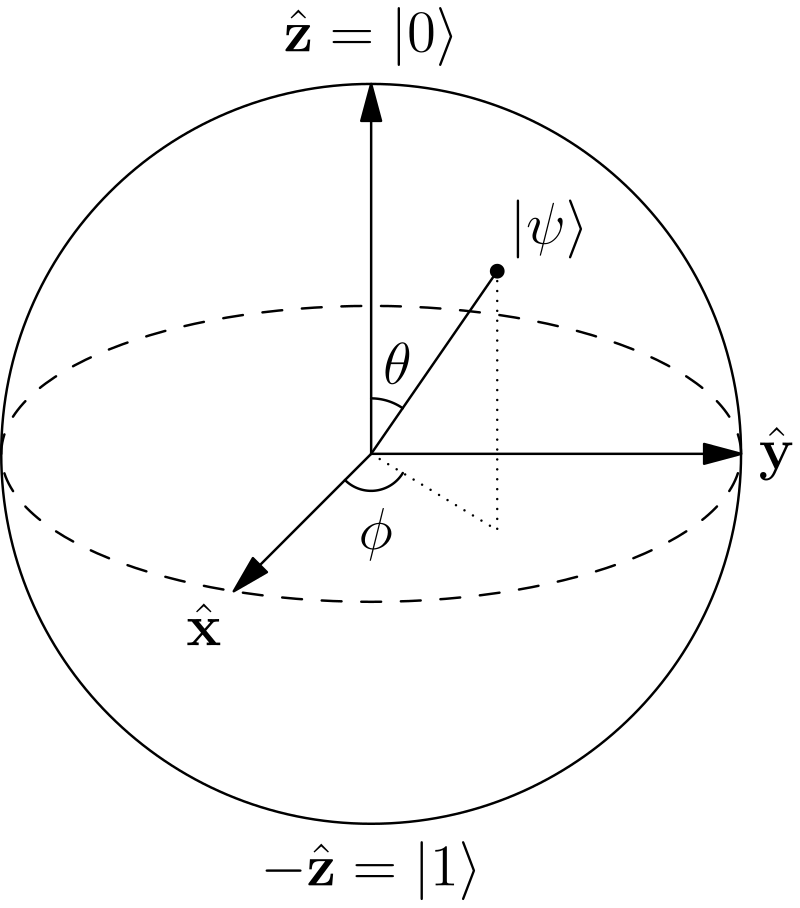
Unlike classical digital states (which are discrete), a qubit is continuous-valued, describable by a direction on the Bloch sphere. Despite being continuously valued in this way, a qubit is the smallest possible unit of quantum information, and despite the qubit state being continuously-valued, it is impossible to measure the value precisely.
Five famous theorems describe the limits on the manipulation of quantum information.
- No-teleportation theorem, which states that a qubit cannot be (wholly) converted into classical bits; that is, it cannot be “read”.
- No-cloning theorem, which prevents an arbitrary qubit from being copied.
- No-deleting theorem, which prevents an arbitrary qubit from being deleted.
- No-broadcast theorem, although a single qubit can be transported from place to place (e.g., via quantum teleportation), it cannot be delivered to multiple recipients.
- No-hiding theorem, which demonstrates the conservation of quantum information.
These theorems prove that quantum information within the universe is conserved. They open up possibilities in quantum information processing.
So, that was all some insight into quantum computers.

