Kepler’s Laws is a set of three astronomical laws that describe the motion of planets around the sun. These laws were published by the German astronomer Johannes Kepler in between 1609 and 1619. He published the first two laws in 1609 in a book called Astronomia Nova while the third law was published in 1619 in a book called Harmonices Mundi.
Though these laws sound very obvious today, back in the 16th and early 17th century it took years of observations to come up with these laws. Kepler derived these laws using his years of observations and lifetime observations made by Tycho Brahe, whom he used to assist.
Kepler’s 3 Laws in simple terms are
1. Every planet’s orbit is an ellipse with the Sun at one of the two foci
2. A line joining the Sun and a planet sweeps out equal areas in equal times.
3. The square of a planet’s orbital period is proportional to the cube of the semi-major axis of its orbit.
So, let us see the three laws one by one in detail
Index
Kepler’s First Law
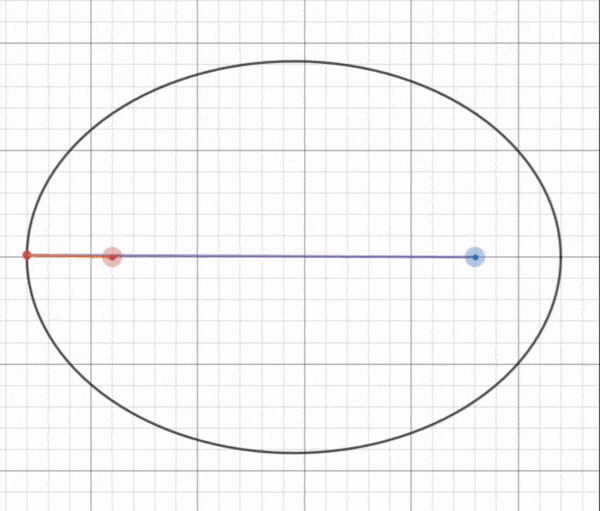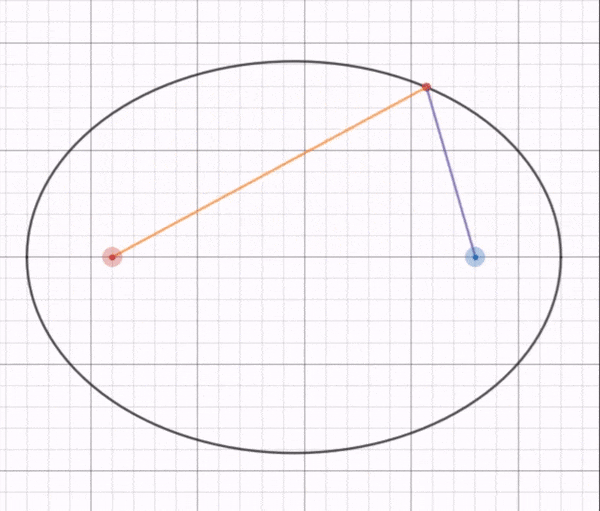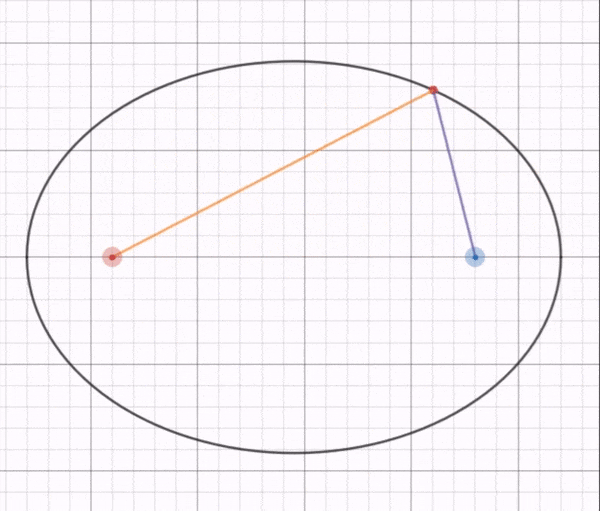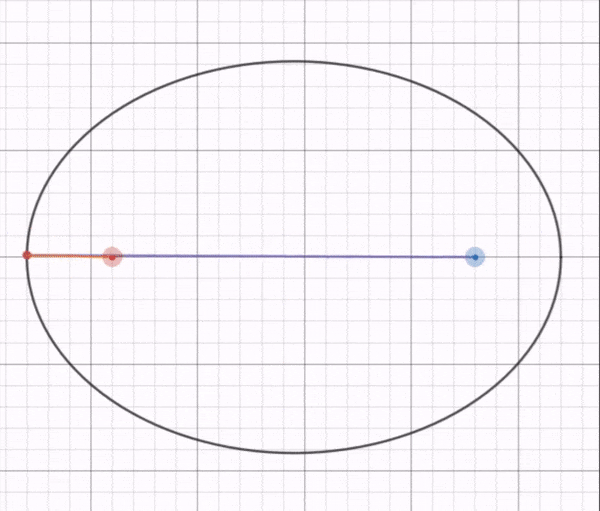
Kepler’s first law of motion or the law of ellipses says that planets are orbiting the sun in a path described as an ellipse with the sun at one of the two foci.
What are Foci?
For two given points, say a and b, an ellipse is a collection of points such that the sum of the distance from every point to a and b is constant. The points a and b are the foci of the ellipse.
It was also observed that the eccentricity of most of the planetary orbits was less due to which the orbits appear nearly circle. For example, the eccentricity of Earth’s orbit is 0.0167
What is eccentricity?
The eccentricity of an ellipse measures how flattened a circle it is. It is equal to the square root of [1 – b*b/(a*a)]. The letter ‘a’ stands for the semimajor axis, ½ the distance across the long axis of the ellipse. The letter ‘b’ stands for the semiminor axis, ½ the distance across the short axis of the ellipse.
How did Kepler formulate the First Law?
Kepler with Tycho Brahe was observing the movement of Mars and after years of observations, Kepler showed that an elliptical orbit would explain the observations much better when compared to a circular orbit. He then extended this elliptical orbit of Mars to all the planets and showed that this all planets orbit Sun in an elliptical orbit. (It was not easy as people like Galileo, Copernicus, and his own master Tycho Brahe believed and supported circular orbits)
Importance
The First Law was important because it cleared a misconception that the orbits are circular. Secondly, it supported the heliocentric model by Copernicus and took humanity towards the right direction in understanding our solar system.
Kepler’s Second Law
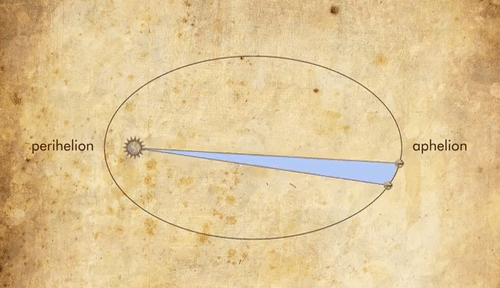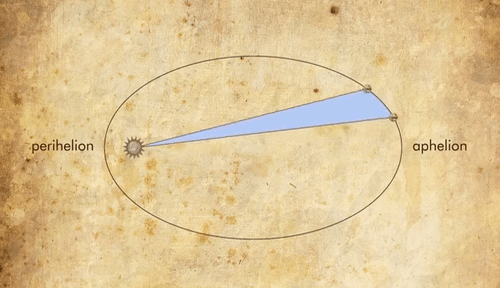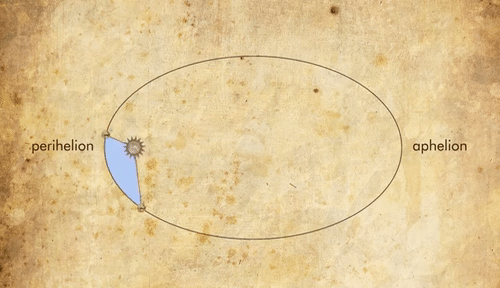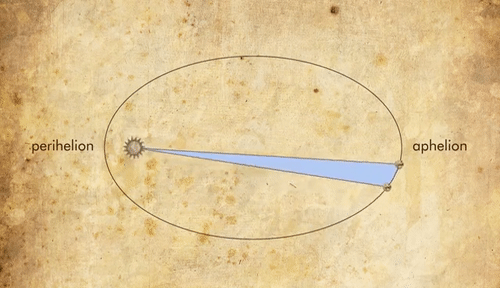
Kepler’s Second Law or the Law of Equal Areas states that a line joining the Sun and a planet sweeps out equal areas in equal times. This means that the speed of a planet changes constantly as it orbits the sun. A planet moves fastest when it is closest to the sun and slowest when it is furthest from the sun.
This inverse relationship between the distance from the sun and the speed was possible only if the orbits of the planets were elliptical because if the orbits were circular the velocity should be constant.
How did Kepler formulate the Second Law?
As mentioned above, Kepler was observing the movements of Mars and the data clearly showed that Mars was changing its speed. It was clear from this observation that Mars cannot have circular orbit and thus Kepler arrived at an elliptical orbit.
Upon keen observation, Kepler found that the area covered by the line joining Mars and Sun between any equal time intervals was the same irrespective of its position. Thus it was understood that Mars moved faster when it was closer to the Sun and moved slower when it was away from the Sun.
So, all this led to the formulation of the Second Law of Planetary Motion.
Importance
Kepler’s second law was also equally important. This law helped Newton while formulating his Law of Gravitation between the planets and the Sun and also between Earth and the Moon.
Kepler’s Third Law
Kepler’s Third Law or the Law of Harmonies states that the square of a planet’s orbital period is proportional to the cube of the semi-major axis (½ the distance across the long axis of the ellipse) of its orbit.
That means
T2/R3 = K (Constant), for any planet
Where
T = Orbital period
R = Semi Major Axis
(T1 / T2)2 = (R1 / R2)3
Where,
T1, T2 = Orbital Periods of Two Planets
R1, R2 = Semi Major axis of Two Planets
Though these ratios have small discrepancies i.e the ratio is not exactly the same for all the planets, the difference is negligible. You can check the values here
How did Kepler formulate the Third Law?
Today, we can derive Kepler’s third law using Newton Law of Gravitation but back then Kepler had no idea about Gravity. He was searching for some relation between the spacing of planets and he finally found this relation between the orbital period and semimajor axis. So, this law was purely based on data at that time.
Kepler even came close to explaining gravity in his book Astronomia Nova, he was not sure about it.
Importance
Third Law of Planetary Motion is very important and helps us explain a lot of problems like
- Determining semi-major axis of Halley’s comet
- Finding most efficient route to Mars
- How far (from the center of Earth) should synchronous satellites orbit?
So, those were the Kepler’s Laws, how were they formulated and their importance. I hope you got a clear idea about these laws, you can always comment your doubts below.