Lens Maker’s formula is a formula that relates focal length, radii of curvature, and refractive index of the lens. As different devices need lenses of different focal lengths, this formula helps lens manufacturers in finding the radii of curvature.
Before understanding the formula, let us look at some terminology you need to know
Prerequisites
Firstly, you need to know that broadly there are two types of lenses namely, convex lens and concave lens.
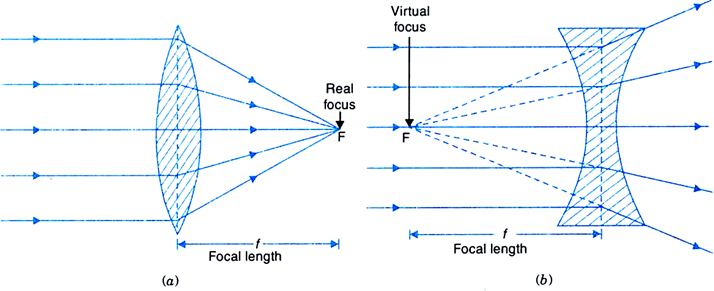
(b) Concave Lens
Convex Lens: An optical lens is generally made up of two spherical surfaces. If those surfaces are bent outwards, the lens is called a biconvex lens or simply convex lens. These types of lenses can converge a beam of light coming from outside and focus it to a point on the other side.
Concave Lens: A concave lens is any lens that has an inward curve in the middle. In other words, the edges of the lens are thicker than the middle. This causes light that enters the lens to spread out, or diverge.
Focal Length (f): The distance between the optic center of the lens and the point where light from infinite source converge or appear to converge after passing through the lens is called the focal length.
Radii of Curvature (R1, R2): Radius of curvature is the radius of that sphere of which the lens is a part. As discussed above, a lens is made up of two spherical surfaces, so, there are two radii of curvatures i.e R1, R2.
Refractive Index (n): It is the ratio of the velocity of light in a vacuum to its velocity in a specified medium. This ratio is called the refractive index of that medium and is a measure of the bending of light when it enters into that medium from vacuum.
The Formula
The Lens Maker’s formula for a thin lens is as follows:
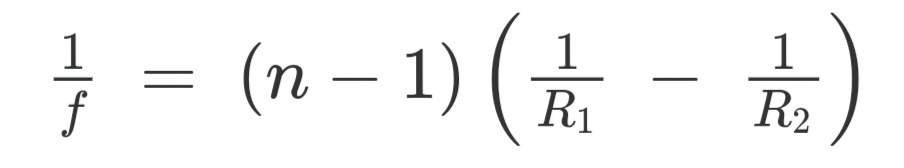
where,
f is the focal length
n is the refractive index of the material used
R1 is the radius of curvature of sphere 1
R2 is the radius of curvature of sphere 2
Sign Conventions
For Convex Lens
R1 is positive, R2 is negative and f is positive
For Concave Lens
R1 is negative, R2 is positive and f is negative
Note: This formula is said to be valid for a thin lens only. A thin lens is that lens whose thickness is very less when compared to the radius of curvature. Basically, when light enters a lens, it undergoes refraction twice, once when it enters and then when it exists. In a thin lens, we can ignore this effect and the above formula comes after ignoring that only.
The formula for a lens with a considerable thickness is as follows:
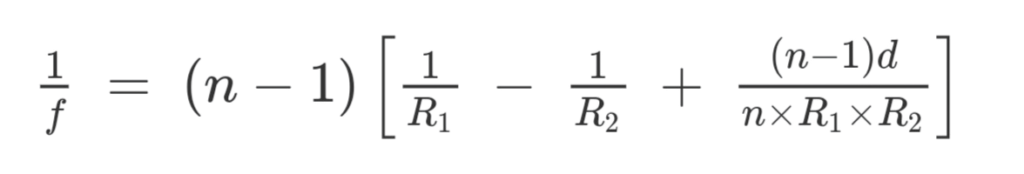
where,
d is the thickness of the lens (This d is comparable to radii of curvature R1 and R2)
The Lens Maker’s Formula when the outside medium is not air or vacuum(for air n=1)
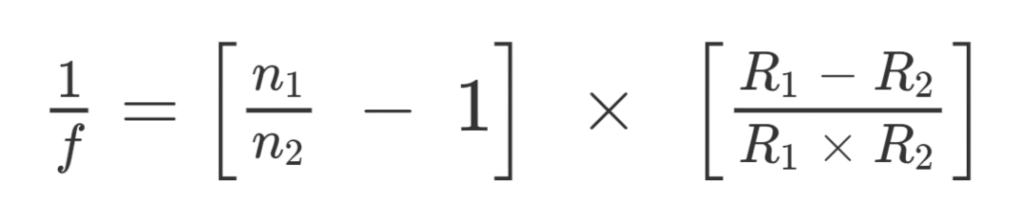
where,
n1 is the refractive index of lens material
n2 is the refractive index of the material outside
So, that was a glimpse about the popular Lens Maker’s formula and if you are interested in the derivation, you can have a look at it here
FAQ
Lens Maker’s formula is a formula that relates focal length, radii of curvature, and refractive index of the lens. This is so-called as the formula helps lens manufacturers in finding the radii of curvature of the required lens.

