Maxwell’s Equations: An Overview

Maxwell’s Equations in electromagnetism are as important as Newton’s Laws in Mechanics. The four equations form the base of classical electromagnetism.

Maxwell’s equations are a set of four equations that describe how electric charges and electric currents create electric and magnetic fields and further describe how an electric field can generate a magnetic field and vice versa.

So, let us look at all the four equations one by one….

Gauss’ Law or Maxwell’s First Equation

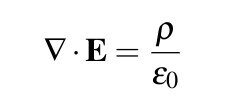
According to Gauss Law, electric charges produce an electric field. The electric flux across a closed surface is proportional to the charge enclosed.

This law relates the distribution of electric charge to the field it creates. If you know the shape of the object and, therefore, how the charge is distributed, you can use Gauss’ law to figure out an expression for the electric field. When there is a degree of symmetry, the equation becomes simpler.

Gauss’ Law or Magnetism and Maxwell’s Second Equation

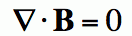
This law states that there are no magnetic monopoles. This law is more of a statement only. We know that charges exist as positive or negative but in magnetism, there is no single pole (north or south), they are always together.

3. Faraday’s Law or Maxwell’s Third Equation

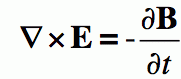
Faraday’s law tells us that time-varying magnetic fields will induce a voltage in the coil. It means that if the magnetic field strength changes, or the magnet moves, or the coil moves, or the coil is rotated. a voltage will be induced in the coil.

Ampere’s Law or Maxwell’s Fourth Equation

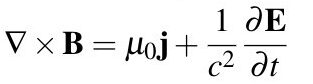
Ampere’s law says that steady current and time-varying electric fields (the latter due to Maxwell’s correction) produce a magnetic field. It tells that the magnetic field created by an electric current is proportional to the size of that electric current, with a constant of proportionality equal to the permeability of free space. Stationary charges produce electric fields, proportional to the magnitude of that charge. But moving charges produce magnetic fields, proportional to the current (the charge and movement).

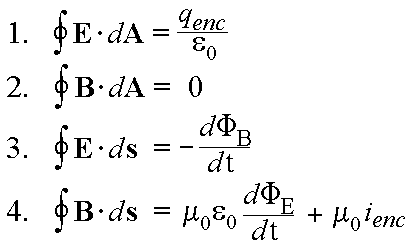
Applications Of Maxwell’s Equations

As we know that Maxwell’s equations form the basis of electromagnetism, thus, there are an uncountable number of application for Maxwell’s equations.

Understanding electromagnetism made us capable to create images of the body using MRI scanners in hospitals. We have created magnetic tape, generated electricity, and built computers. Any device that uses electricity or magnets is built upon the original discovery of Maxwell’s equations.

So, I hope you got a glimpse of Maxwell’s equations and their immense importance.