Newton’s Law of Gravitation is a theory that explains how all objects with mass interact with each other. It provides a mathematical framework to make quantitative calculations about this interaction too. It is one of the most successful theories of gravitation.
Index
The Law
Newton’s Law of Gravitation was originally stated as follows:
Any two particles in the universe attract each other with a force proportional to the product of their masses and indirectly proportional to the square of the distance between them.
Mathematically, the force can be written as

Where
m1 and m2 are the masses of the two particles
r is the distance between them.
As we have seen, there is a need for a proportionality constant to make this a complete equation. The proportionality constant, G, is called the universal gravitational constant and was experimentally obtained by Cavendish in 1798. It is equal to 6.67259 x 10-11 N m2/kg2.

In a more modern, vector form, the equation can be written as:
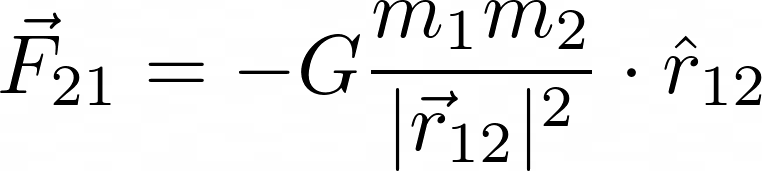
This contains the same meaning as the original equation of Newton’s, with the usage of the subscripts and vectors showing that the force is attractive and acts along the line joining the particles.
Newton’s law of gravitation originally seems to cover only particles (in modern terms, point masses), i.e. particles so small that they take up only a point of space and are not spread out. For any larger bodies, such as those we encounter in daily life, one needs to integrate over both the bodies to obtain the full expression for the force between them.
One of Newton’s greatest achievements was to extend this law to large bodies by the use of integral calculus. Specifically, he showed that spherical bodies, such as planets, behave as though they are point masses located at the center of the sphere.
He also showed with the use of his shell theorem that inside a sphere, the gravitational force depends only on the part of the sphere that is interior to the point in question.
With the help of this law, Newton could explain the gravitational behavior of all objects with masses, regardless of whether it is an apple falling to the ground or planets orbiting the sun.
Historical Backdrop
Before Newton’s advances, Aristotle’s ideas were deep-rooted in the scientific community. When it came to the field of mechanics, the major guiding ideas were of “natural states”. Objects were supposed to go to their respective natural states of rest, with no explanation as to why these states were preferred.

Influenced by the work of prominent scientists, Galileo amongst them, Newton worked on providing a more scientific explanation of the concepts of rest and motion with his three laws of motion. They went on to become the mainstay of mechanics for the next two centuries.
Newton’s law of gravitation was a major leap in scientific terms because it unified terrestrial phenomena such as falling objects with celestial phenomena such as the motion of planets. Its development was foreshadowed by many scientific discoveries along the way.
Galileo and other experimental physicists had performed observations regarding free fall of objects that helped show that their acceleration was a constant. These raised interesting thoughts about the nature of the force that makes the objects fall.
Around the same period, Johannes Kepler, an astronomer, made observations regarding the motion of planets around the sun and stated three laws, which came to be known as Kepler’s Laws of Planetary Motion. The reason, or the force, for this motion, was not yet discovered. Many scientists, such as Hooke, suggested an inverse square law, which Newton himself later used in his law of gravitation.

The Newton’s great success lay in unifying these two seemingly unrelated phenomena – the falling motion of objects and planetary motion – with a single law.
He managed to explain all of Kepler’s laws regarding planets, as well as justify Galileo’s observations regarding free fall. His theory could also make predictions about planetary motion as well.
Evidence in Favour
Most terrestrial phenomena regarding free-fall were already well-explained by Newton’s law of gravitation when taken along with his three laws of motion. Some of the most spectacular evidence in favor of his theory came via celestial observations, with the prediction of the existence of Neptune being prominent amongst them.
Prior to the 19th century, Uranus was the furthest planet known to humankind. Disturbances in its orbit, however, suggested that there was a large body nearby that was gravitationally interacting with Uranus and changing its orbit slightly. Analysis of the disturbances in the orbit based on Newton’s theory of gravitation led to the prediction of a new planet, which was visually confirmed in 1846. This went on to be named Neptune.
Modern Standpoint
Newton’s theory was a great approximation for its times and stood strong for over two centuries. However, just like Newton’s laws of motion were superseded by Einstein’s Special Theory of Relativity, Newton’s law of gravitation has been superseded by Einstein’s General Theory of Relativity: a relativistic theory of gravity that explains many phenomena that Newton’s theory falls short on, such as gravitational lensing of light and discrepancies in the orbit of Mercury.

Nonetheless, it remains accurate to a good approximation and can still be used in cases where relativistic effects are negligible: where the speeds are much less than that of light and gravitational potential is low. As such, it is applicable for most day-to-day phenomena and is basically a simplification of Einstein’s theory in limits of low gravity.

