Kirchhoff’s Circuit Laws are two laws that help us analyze electric circuits in terms of their voltage and current.
The two corresponding laws are hence called Kirchhoff’s Current Law and Kirchhoff’s Voltage Law. They are applicable for most day-to-day usage of electric circuits, though they have their limitations.
Index
The Laws
Gustav Kirchhoff arrived at these laws around 1845 by extending the work of Georg Simon Ohm on circuits. They can be arrived at by simplification of Maxwell’s equations by applying a few limitations.
Kirchhoff’s Current Law
In simplest terms, this can be stated as follows.
The total current entering a point is the same as the current leaving it.
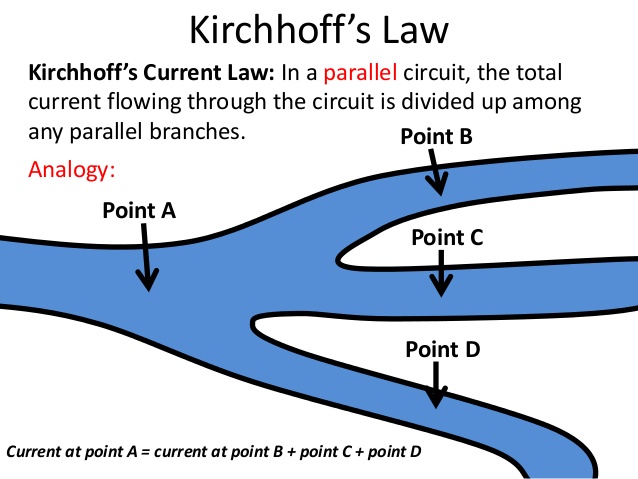
This can be understood as a result of the fact that there are no sources or sinks of charge. If the current is compared to a smoothly flowing stream of water, it makes sense. There would be no point where the amount of water flowing in is not equal to the amount of water flowing out, because water isn’t pooling up anywhere in the flow.
Similarly, in a branch in a circuit, there is no electric charge pooling anywhere and hence the current flowing is the same as the current going out.
Practically, this is applied to junctions(nodes) where two or more branches of the circuit meet. There, we calculate the current flowing in and and out, and assign variables where necessary.
Kirchhoff’s Voltage Law
Kirchhoff’s voltage law can be stated as
The total voltage drop over a closed loop is zero.
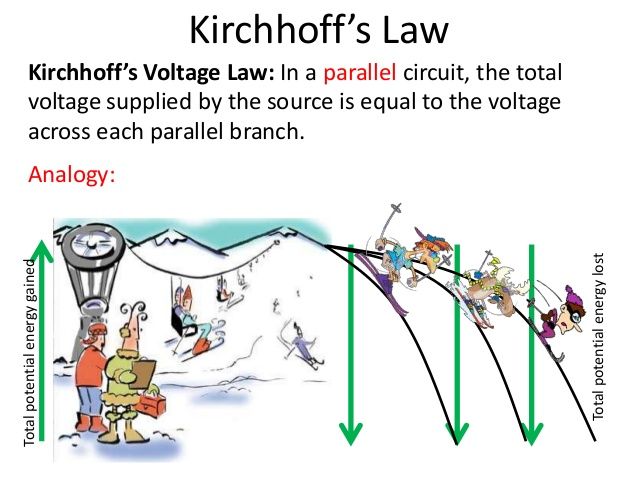
While Kirchhoff’s Current Law is a consequence of the conservation of electric charge, Kirchhoff’s Voltage Law is a consequence of energy conservation (in conservative electric fields).
The basic premise is that there is no voltage drop over a closed-loop because the electric field is conservative.
This means that when we go around a closed path in such an electric field, no work is done in the physicist’s sense. Thus, there is no voltage drop either, as voltage drop is directly related to work done.
The Laws in Action
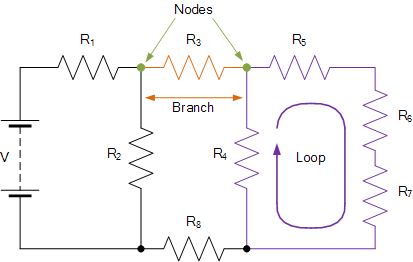
Practically, we use these two laws together.
The current law is used to assign values of current to each branch of the circuit. Then, the voltage law is used over closed loops to associate the various currents with other elements (voltage drops over resistances, etc). Together, they set up a system of equations for the variables of the circuit. These can be solved by mathematical approaches such as the matrix method.
Limitations
Kirchhoff’s laws can be applied only when the circuit behaves in what is called a “Lumped Element Model”. This is an idealized system where the elements like resistances, inductances, etc have only the ideal properties. When this does not happen (such as when there are high-frequency oscillations of the electric field, etc), Kirchhoff’s Laws do not hold.
They can still be used as approximations in some cases, but these require further techniques.
One prominent case where Kirchhoff’s Laws fail is where there are time-varying magnetic fields. These introduce non-conservative electric fields which would conflict with the Voltage Law. Such more advanced cases are dealt with more complex problem-solving methods.
FAQ
It states that The total current entering a point is the same as the current leaving it.
It state that The total voltage drop over a closed loop is zero.

