Sound, in terms of physics, is a wave. It produces a sense of hearing upon reaching the auditory organs of living organisms.
At its very root, however, it is a wave that is transmitted by vibrations of molecules and carries energy. It is produced by the vibrational behavior of a source and is transmitted by pressure changes in the medium surrounding it.
Like waves in general, sound waves also have a wavelength, frequency, and crucially, speed. It is this speed – the speed of sound – at which the wave moves and carries energy.
Before we see how the speed of sound can be found, let us know more about how sound propagates.
Index
Mechanics of Sound Production And Propagation
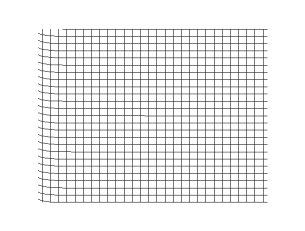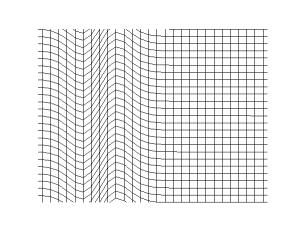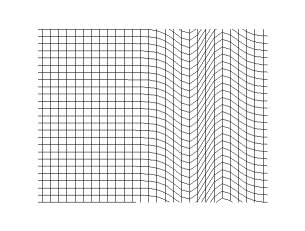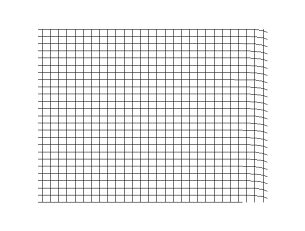
There are two kinds of waves – longitudinal and transverse. In longitudinal waves, the oscillation happens in the same direction as the wave’s propagation. In transverse waves, the oscillation happens perpendicular to the wave’s propagation.
The two kinds of waves, in 2D

Longitudinal Waves 
Transverse Waves
Sound waves are longitudinal in all media, solid, liquid, or gas. Further, they can also be transverse waves in solids.
The reason for this lies in the propagation mechanics of sound waves. Sound waves move as pressure variations in the medium and are maintained by the inner elastic forces of the medium. For gases and liquids, the only elastic forces are caused by the compressibility of the medium. As compression happens in the same direction as propagation, only longitudinal waves are possible in gases and liquids.
As we observe here, the moving source (red) produces disturbances in the particles of the surrounding medium. This disturbance is carried on as a pressure variation throughout the medium as the source keeps moving back and forth.
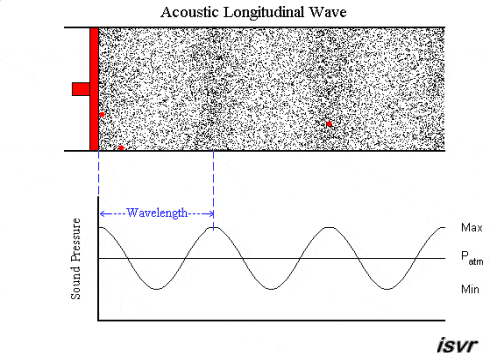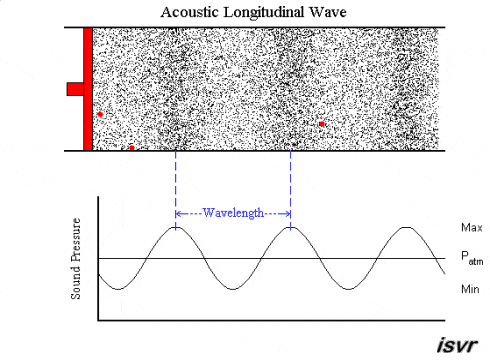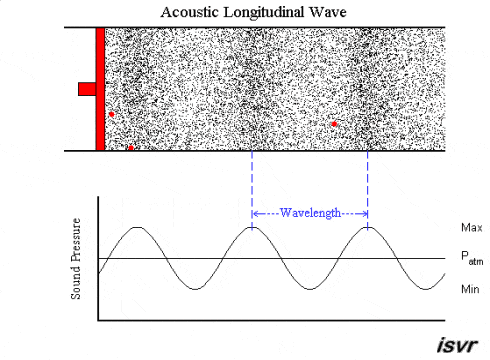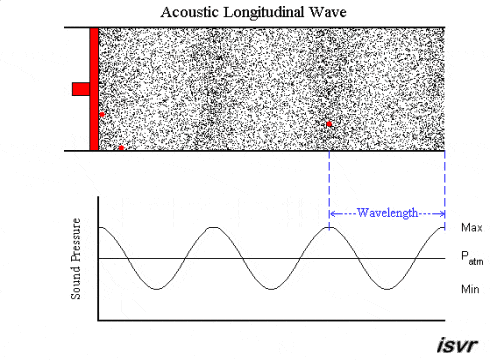
Solids, however, have an extra source of elastic force in them. This is the shear modulus, which gives rise to stress in the direction perpendicular to the motion of the wave. As a result, we can observe transverse waves, in addition to longitudinal waves, in solids.
Relevant physical quantities
As we’ve already seen, the propagation of sounds requires elasticity of the medium. This elasticity is measured by elastic moduli, which are physical quantities that measure how elastic a given medium is.
For longitudinal waves, the oscillations are in the same direction as the motion of the wave. This makes the required elastic modulus in this case the bulk modulus K (also called B). The bulk modulus measures how much a material resists compression along the direction of force applied.
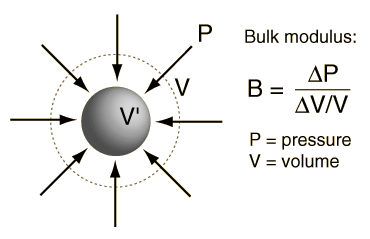
K is the only relevant elastic modulus for liquids and gases, as they can offer resistance only along the direction of compression.
Solids, however, offer resistance also perpendicular to the direction of the force. This gives rise to the possibility of transverse sound waves. The relevant modulus of elasticity in this case is the shear modulus G, which measures the resistance a solid gives perpendicular to the direction of force applied.
In general, regardless of whether bulk modulus or shear modulus is considered, sound travels faster in more elastic media.
Another important physical quantity is density, ρ, which determines how inertial (opposed to motion) the material is. In general, with all else being equal, sound travels slower in a denser medium.
Do note that sound travels faster in solids than in liquids or gases even though solids are denser. This is simply because solids also have extremely high elasticity which compensates for their higher density.
Experimental History
People have performed several experiments to measure the speed of sound in air, starting from the medieval ages. One of the earliest experiments was performed by Pierre Gassendi in the 17th century. He asked for another person to fire a gun far away. He then checked the time difference between seeing the gun flash and hearing the sound of the shot. Because he knew the distance to the gun, he could get a rough measure of the speed of sound, which was not accurate because of errors in time measurement.
Later, Sir Isaac Newton performed an experiment involving echos, which gave him a closer estimate of the speed of sound in air, which was still around 15% away from the actual value. He went a step further, however, and derived a formula for the speed of sound.
The speed of sound in air formula
Since sound is a wave, its speed depends on two quantities – an inertial quantity and an elastic quantity. For a generalized wave, these quantities are related to wave speed as:
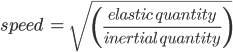
Newton initially considered the elastic quantity to be pressure (P) and the inertial quantity to be density (ρ) of air. As a result, the formula he arrived at for v, the speed of sound, was
v = √(P/ρ)
Later research showed this formula was incorrect because he assumed sound waves to spread isothermally. In reality, sound waves spread adiabatically as they do not get to exchange heat with their environment. With this correction by Laplace, the correct formula for the speed of sound in the air became
v = √((γP)/ ρ)
Where P and ρ represent the same quantities of pressure and density, while γ is the adiabatic index, equal to around 1.4 for air. The quantity in the numerator, γP is often simply called Ks, the isentropic bulk modulus, another measure of elasticity.
Using the ideal gas equation PV = nRT for air, we can replace pressure P with temperature T to obtain
v = √((γRT)/M)
Where R is the universal gas constant, a thermodynamical constant, and M is the molecular mass of gas.
Derivation
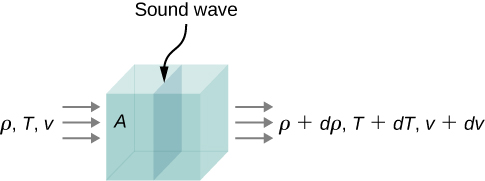
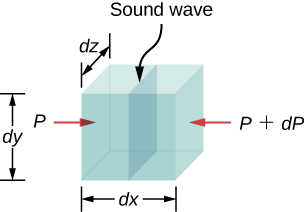
For the derivation of speed v, consider an infinitesimally small cuboid of air (density ρ and pressure P) with cross-sectional area A. Let the wave propagate in the x-direction. Since it is a fluid, by the principle of continuity, the mass entering one side must equal the mass exiting the other side. Thus, mass flux j = ρv must be a constant, which gives, upon differentiation,
ρ dv = -v dρ … (1)
Now, the force F exerted on the cuboid of air is due to pressure difference dP across the front and back of the cuboid, multiplied by cross-section area. Thus,
F = – dP . A
Now, by Newton’s law,
F = ma
Where m is the mass of the air and a is its acceleration. Comparing the above two equations, we get,
ma = -dP . A
Since mass is volume times density, we can write m = ρV = ρ A dx, where dx is the length of the tiny cuboid and A is the cross-section area. Also, the acceleration a can be written as a = dv/dt so we rewrite the above equation as
(ρ A dx) dv/dt= -dP A
Simplifying the algebra, we get
dv = -dP/ρ (dt/dx)
Taking v = dx/dt and substituting, we get
dv = -dP/ρ(v)
Which gives
v( ρ dv) = -dP
Again we use the equation of continuity (1) ρdv = -vdρ to replace ρdv in the left-hand side to get
v (-v dρ) = – dP
v2=dP/dρ
Thus,
v = √(dP/dρ) ….(A)
To obtain the formula in its final form, we must replace dP/dρ in the right-hand side with a term related to the adiabatic process. For this, we note that in an adiabatic process, where γ is the adiabatic index.
PVγ= const.
Simplifying via logarithmic differentiation and eliminating constants, we get
dP/dρ=(γP)/ρ
So finally substituting this result in the equation (A) for velocity, we get
v = √(γP/ ρ)
Which is the required result.
Speed of sound in other media
We can use similar ideas of wave speed to obtain the speed of sound in other media such as solids and liquids. The general idea of
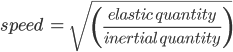
still holds, and the only changes we make are in choice of elastic and inertial quantities. We skip the derivations for simplicity, and provide the results here.
For longitudinal sound waves in liquids, where K is bulk modulus and ρ is density,
v = √(K/ρ)
For solids, there are both longitudinal and transverse sound waves, called primary and secondary waves respectively. Thus there are two velocities, vp and vs corresponding to them.
For primary (longitudinal) waves, both the bulk modulus K and shear modulus G are involved as elastic quantities, and the formula becomes
vp= √((K+(4/3.G)) / ρ)
For secondary (transverse) waves, which oscillate perpendicular to the direction of propagation, only shear modulus G is relevant, and thus we get
vs= √(G/ρ)
Conclusion
We have seen how sound propagates in various media, and how this method of propagation gives rise to a measurable speed of sound. We have also seen how this speed of sound can be calculated theoretically, and seen the derivation of the speed of sound in air formula.