The early 20th century has seen a lot of revolutionary experiments, equations, and theories. One such important equation was the Schrodinger Equation. This is a very important equation in Quantum Theory.
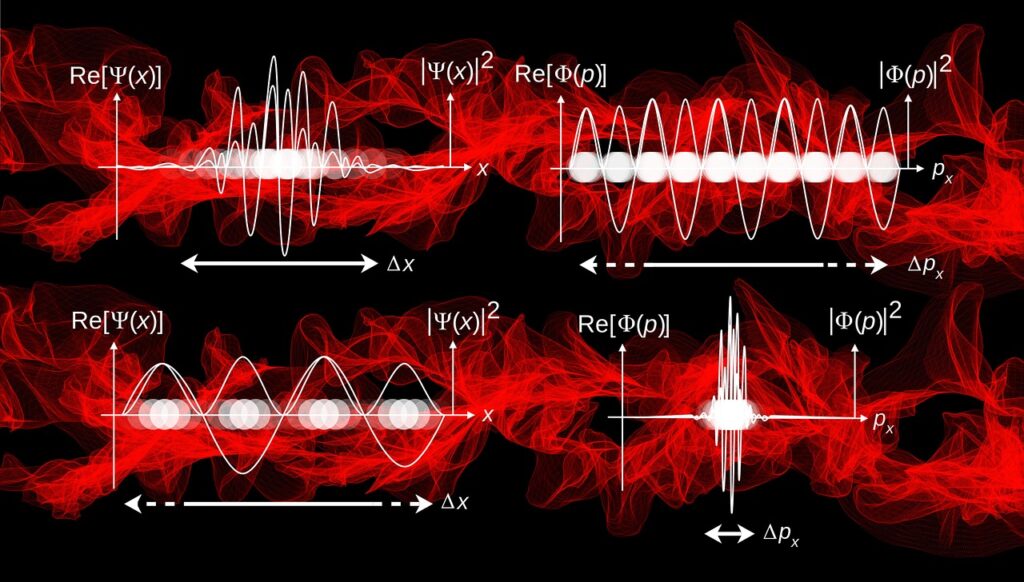
Schrodinger equation is a partial differential equation that describes the form of the probability wave that governs the motion of small particles, and it specifies how these waves are altered by external influences.
History
The roots of this equation lie in the double-slit experiment on electrons performed by two physicists named Davisson and Germer. It resulted in electrons showing wave nature. An electron that was considered a particle till then showed the properties of a wave.
Another Physicist Max Born suggested that this wave was not a normal wave rather it was a probability wave wherein the probability of an electron existing at one place is dependant on the wave size.
Erwin Schrödinger came up with an equation that described these electron waves with pretty good accuracy.
Let us look at the equation itself now
There are two types of Schrodinger Equation and they are
- Time-Independent Schrodinger Equation
- Time-Dependent Schrodinger Equation
The time-dependent Schrödinger equation, as its name says, describes the motion of a matter-wave which varies with time:


where,
ℏ is the reduced Planck constant,
m is the electron mass,
∇2 is the Laplacian operator,
r is the position (x,y,z)
Ψ is the wave function,
V is the potential energy,
Ĥ is the Hamiltonian operator (Energy Operator)
The time-independent Schrödinger equation describes the motion of a matter-wave which does not vary with time:
In this case, the potential energy also does not vary with time.

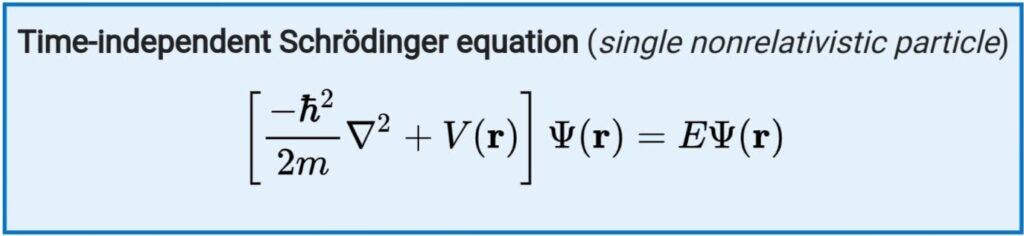
where,
ℏ is the reduced Planck constant,
m is the electron mass,
∇2 is the Laplacian operator,
Ψ is the wave function,
Ĥ is the Hamiltonian operator (Energy Operator)
E is a constant equal to the energy level of the system
Let us not get into complex explanations of this equation. Instead, let us know why is this equation so important.
This equation in Quantum Mechanics is as important as Newtons Laws in classical physics
Let us look into the applications and predictions by this equations
- The first and most important implication of this equation is that it gives us a boundary where the electron can be present. With its position and momentum completely unpredictable, even getting a boundary is a lot. By solving the equation, you basically get a probability distribution of an electron depending on it’s three quantum numbers (n, m and l)
- The time-dependent general equation is used throughout quantum mechanics, for everything from the Dirac equation to quantum field theory, by plugging in diverse expressions for the Hamiltonian.
- Schrodinger Equation also predicts Quantum Tunneling.
I hope you got a basic knowledge of Schrodinger’s equation.