The Poiseuille equation (also called Hagen-Poiseuille equation) is a fluid mechanical equation that helps us understand how pressure varies in a flowing liquid.
Specifically, it deals with pressure drops in viscous, Newtonian, incompressible fluids showing non-accelerated laminar flow (i.e. the flow is smooth and not turbulent like in a fast-moving river).
It has specific limitations, such as that it can be used only for long tubes that are cylindrical in shape, with a uniform radius. Under these constraints, it is a really useful predictor of physical values.
Index
The Equation
Poiseuille’s equation, in mathematical form, is stated as
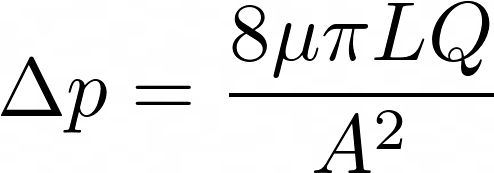
where,
∆p is the pressure drop
μ is the viscosity of the fluid
L is the length of the tube
Q is the flow rate
A is the cross-section area of the tube.
Physical Background
For a viscous incompressible fluid, there are two main forces involved in its flow namely
1. Pressure difference
2. Viscous drag.
The pressure difference is what gives the “push” for the liquid to flow, while the viscous drag force tries to slow it down. In the equilibrium, both forces are in balance, and there is no acceleration of the fluid.
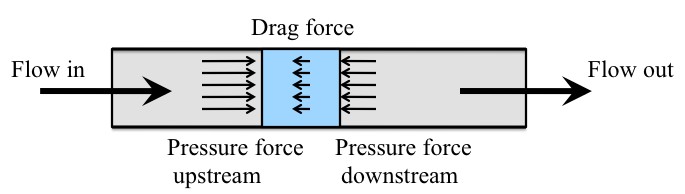
Pressure difference exerts a force that is proportional to the cross-section of the tube. This is simple enough to visualize, as pressure itself is defined as force per area.
Viscosity is a bit trickier to visualize. Think of the fluid consisting of concentric cylindrical layers. As viscosity is a drag force, it makes the outermost layer of the fluid “stick” to the surface of the tube. The inner layers move faster than the outer ones. Any one cylindrical layer in between is sandwiched between a slower moving outer layer and a faster-moving inner layer. Both exerted a viscous drag on it.
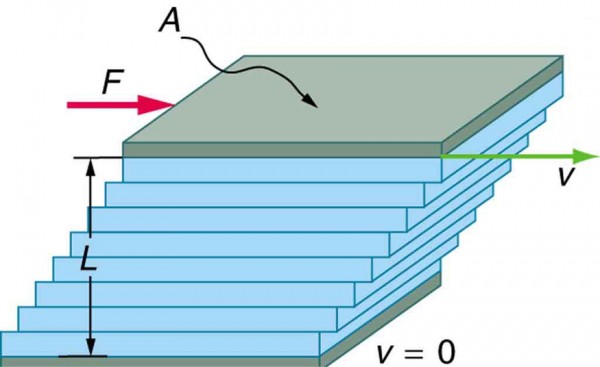
Writing the mathematical equations for these forces and equation them, we can cancel similar terms and arrive at the above expression for pressure difference.
Alternate Derivation
A more direct but also mathematically involved derivation of the same law uses the Navier-Stokes equations that deal with fluid dynamics. Using the correct mathematical forms of the conditions (incompressibility, Newtonian behavior, etc) we directly can arrive at the same results.
Applications
As we have seen, Poisueille’s equation applies to incompressible Newtonian fluids flowing along long cylindrical tubes in a steady, non-turbulent manner. It is used to model several fluid flows in biology and medicine.
Examples include blood flow in capillaries, fluid flow in insect probosci, and intravenous flow in cannulas.
However, it might not be an accurate descriptor in all cases, as it has some limitations addressed below.
Limitations
Poiseuille’s law, in its original form, can be used only for Newtonian fluids in tubes whose length is much more than the width.
The steady-state described above won’t be met and the equation will not be valid if the tube is too broad or length too short. For similar reasons, it cannot be used for the initial part of the flow.
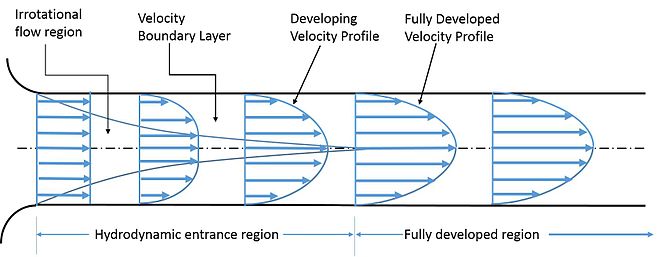
Another limitation with regard to breadth is that the law is valid only when viscosity plays a sufficient role in the fluid flow. When the tube is very broad, viscosity has a prominent effect only at the edges, and the central part shows behavior different from the experimental suggestion.
However, the law can be modified to understand certain deviations from the initial case. These include rectangular cross-sections, and changing pressure differences.
Naturally, for non-Newtonian and incompressible fluids, the law does not hold at all.
Other laws such as the Darcy-Weisbach equation deal with the more complicated cases of fluid flow.

