Bohr’s Atomic Model

Bohr’s Atomic Model was introduced by Niels Bohr in 1915. It was basically a modified version of Rutherford’s Atomic Model wherein Bohr explained that electrons move in fixed orbitals (shells) and not anywhere in between and he also explained that each orbit (shell) has a fixed energy level.

Let us look at a bit of history and then get into the details of this model.

Before Bohr

Research, experiments, and theory into the atomic structure have resulted in much understanding of the stuff that makes us.

Dalton’s Atomic Theory, which stated that atoms are indivisible was shattered with the discovery of subatomic particles, which make up the atom. Discovery of the proton, electron, and neutron, made us wonder, what does the atom actually look like? With his classic, Alpha Ray Scattering Experiment Rutherford was able to suggest a possible model for the atom.

The Rutherford Atomic Model placed the protons and neutrons inside a small structure called the ‘nucleus’ with the electrons revolving around the nucleus in circular orbits. It was like our solar system, with planets revolving around the sun, a beautiful symmetry that sadly wasn’t feasible.

Maxwell’s Laws of Electrodynamics suggest that a charged particle moving in a circular orbit releases energy in the form of electromagnetic radiation.

Thus, negatively charged electrons would emit energy as they revolve around the nucleus, with its orbit decreasing with time. The electron spirals moving closer to the nucleus eventually would collapse into it in what calculations suggest a time of 10^-8 s. 

But life still lives on. Atoms don’t form and simultaneously blow up. As a result, Rutherford’s Atomic Model doesn’t work. Then enters Bohr.

Bohr’s Assumption

Bohr’s Atomic Model was for the hydrogen atom and hydrogen-like species(species with only one electron). Hydrogen Bohr model was based on some assumptions which are listed below:

1. The singular proton of the hydrogen atom or the protons and neutrons of the hydrogen-like species(ex- He⁺, Li²⁺, etc.) are present in the centre of the atom, in a positively charged nucleus.
2. The electron revolves around fixed circular paths of fixed radius and energy called stationary states. An electron revolving in these fixed circular path doesn’t radiate energy as per Maxwell’s laws and maintains a constant energy value. So, these are called the stable orbits and they have quantised energy.
3. The energy of the electron changes only when it makes transitions from the energy level of one stationary state to the energy level of another stationary state.
4. Bohr’s Quantization Principle defines these stationary states as circular paths on which the angular momentum of the electron is an integral multiple of h/2π.

Formulas for Bohr’s Atomic Model

Deriving Bohr’s Quantization Principle

Bohr’s Quantization Principle can be derived using the de-Broglie Equation. The de-Broglie Equation states that :-

λ =h/mv 

where,
λ is the wavelength of the matter-wave
h is the Planck’s Constant
m is the mass of the body
v is the velocity of the body 

For a circular path of radius r
The circumference is C = 2πr
For an electron with a de-Broglie wavelength of λ, for it to maintain a sustained wave the wavelength should be equal to the circumference of the circular path. Let there be n wavelengths, thus – 

2πr = nλ

⇒ 2πr = n(h/mv) [using de-Broglie wave equation :- λ = h/mv]

⇒ mvr = n(h/2π) [The angular momentum of an object L=mvr]

= L = n(h/2π)

where,
L is the angular momentum of the electron the circular path
n is any integer

Therefore we have derived Bohr’s Quantization Principle, and have defined the stationary state.

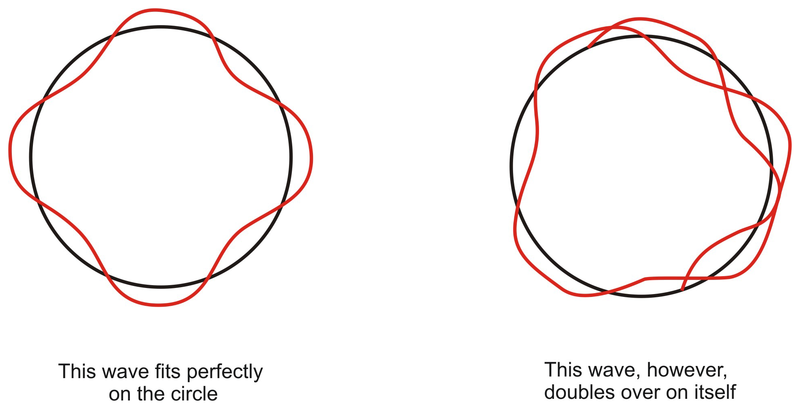
Deriving Radius of a Stationary State

For a body moving in a uniform circular motion, a centripetal force acts on it maintaining the circular motion. This centripetal force can be stated in the form of an equation as,

F = mv²/r

where,
m is the mass of the body
v is the velocity of the body
r is the radius of the body

In a hydrogen atom or a hydrogen-like atom the centripetal force is maintained by the electrostatic force of interaction between the electron and the protons. There are Z number of protons in an atom. Z represents the atomic number of the atom. 

The electrostatic force between the electron and the protons comes out to be:-

F = k(q₁ q₂/ r² )

where,
k is equal to 9.0 x 10⁹ N • m² / C²
q₁ is the charge of the electron which is 1.6 x 10^-19 C
q₂ is the charge of the protons which is Z x 1.6 x 10^-19 C
r is the distance between the protons and the electrons, in this case, the radius of the circular orbit

Since the electrostatic force acts as the centripetal force here we can equate both the equations as:-

mv²/r = k(q₁ q₂/ r² )

From the Bohr’s Quantization Principle we have :-

L = n(h/2π)

⇒ mvr = n(h/2π)

⇒ v = n(h/2πmr)

Therefore, we can proceed as:-

mv²/r = k(q₁ q₂/ r² )

⇒ (m/r) (n²h² / 4π²m²r²) = k(q₁ q₂/ r² )    [Using v=nh2mr]

⇒ n²h²/4π²mr = kq₁q₂

= r = n²h² / 4π²kmq₁q₂

Replacing the values as stated above and putting the mass of an electron as 9.1 x 10^-31 kg we get :- 

r = (n²/Z)52.9 pm

For the first orbit of the hydrogen atom, n = 1 and Z = 1, we have r = 52.9 pm which is called the Bohr Radius.

Deriving Velocity of an Electron in a Stationary State

From the Bohr’s Quantization Principle we have :-

L = n(h/2π)

⇒ mvr = n(h/2π)

⇒ v = n(h/2πmr)

Since r = n²h² / 4π²kmq₁q₂ we can replace this in the above equation to give us:-

⇒ v = 2πkq₁q₂/nh

Putting in the values discussed above into the equation above we get :-

v = 2.19106(Z/n) m/s

Deriving Energy of an Electron in a Stationary State

The kinetic energy of the electron is :-

KE = mv²/2

Which on putting the values for the mass of the electron and the general equation for the velocity of the electron in the n^th stationary orbit we get:-

KE = 13.6(Z²/n²) eV

The electric potential due to the nucleus at a point a distance r from it is :-

V = kq₂/r

Therefore the potential energy of the electron is :-

PE = Charge on electron Potential of the electron

⇒ PE = – q₁ k(q₂/r)

⇒ PE = -kq₁q₂/r

Replacing the general equation for the radius of the n^th orbit and the values of q₁ and q₂ discussed above we have potential energy as :-

PE = -27.2(Z²/n²) eV

The total energy of the electron therefore comes out to very simply :-

TE = KE + PE = 13.6(Z²/n²) eV – 27.2(Z²/n²) eV

TE = -13.6 (Z²/n²) eV

Success of Bohr

Bohr’s theory was able to account for the stability of the atom, something which the previous model (Rutherford’s model) failed in. Moreover, it was extremely robust and could give us a lot of information.

It agreed with the experimentally obtained results of the hydrogen line spectra. Since we knew the various energy levels of the stationary states, we could predict the energy differences and hence the energy released or absorbed when an electron transitioned from one state to the other. Each line spectra accounted for a particular transition. This helped predict values for the line spectra which agreed with the experimentally obtained values hence proving and further strengthening the Bohr Atomic Model.

Bohr’s theory was indeed revolutionary and gave us a very concrete model of the atom.

Failures of Bohr

The Bohr Model met with a lot of problems sadly. These failures eventually resulted in abandoning this theory, and the development of the quantum mechanical model of an atom.

Some of the major failures that the Bohr’s Atomic Model faced are listed below. They are:- 

1. Bohr’s Atomic Model failed for many-electron species. Any atom with more than one electron couldn’t fit into the theory.
2. As spectroscopy techniques improved, what previously seemed like a single line spectrum was seen to be made up of closely spaced lines ( for example, doublets, triplets, etc.). This couldn’t be explained by considering transitions between Bohr stationary states.
3. The splitting of the spectral lines in the presence of an electric field (Stark Effect) and in the presence of a magnetic field (Zeeman effect) couldn’t be explained by Bohr and couldn’t be accounted for by the Bohr Atomic Model.
4. The development of the Heisenberg’s Uncertainty Principle which prevented us from knowing the exact position and velocity of a moving particle simultaneously and accurately meant that it was not feasible to measure and predict the velocities of the electrons and the radii of the stationary states.
   Bohr’s Model didn’t agree with the results of Heisenberg’s Uncertainty Principle.

Conclusion

Bohr’s model remains an important stepping stone towards the development of a picture of an atom. Despite being wrong it still is a simple way to calculate certain values for an atom, an aspect which is a result of its robustness. It is something which bears use even today, especially while understanding the line spectra of hydrogen and hydrogen-like species. 

Bohr’s idea was so influential that it resulted in the classical imagery of the atom, something which is recognised by the masses as what an atom looks like, despite it being wrong. This is a testament to how revolutionary and powerful the idea was.

FAQ