Dirac equation is a fundamental cornerstone of quantum field theory. It helps us understand the behavior of all spin 1/2 particles with mass such as electrons, protons, and fermions (matter particles) in general. It is as important to the understanding of QFT as Schrodinger’s equation is for the understanding of quantum mechanics.
Index
Background
The branch of physics that dealt with objects moving close to the speed of light, special relativity, was developed by Einstein in 1905. Quantum mechanics (the branch of physics that deals with extremely small entities) was developed separately by Schrödinger and Heisenberg in 1926.
However, there were situations where the two fields overlapped. An example was that of the tiny electron orbiting very fast around the nucleus. At that time, around 1926, there was no satisfactory physical theory that explained such situations.

Early attempts were made by Oskar Klein and Walter Gordon in the same year. They made use of Schrödinger’s equation
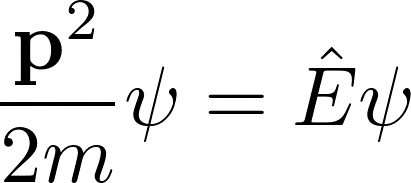
in a fundamental equation of relativity
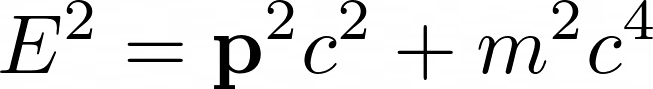
and simplified, to obtain a wave equation.
Where,
E stands for energy
p for momentum
m for mass
c for speed of light.
They suggested that this equation, later called the Klein-Gordon equation, could be used to describe relativistic electrons.
However, the equation made no reference to spin of an electron, which is an intrinsic property of it. Furthermore, notice the presence of squares for the energy (E) and related terms. This gave rise to what mathematicians call a second order differential equation, which raised theoretical problems with regard to relativity. Thus, the Klein-Gordon equation was considered unsatisfactory for describing electrons.
Dirac’s Developments
Paul Dirac tried to find a way out of the problem involving second-order differential equations by taking a square root of the energy (E) from the above expression. The route to the required square root was not easy, as any factorization had to satisfy certain special criteria. Dirac, perhaps inspired by similar work on the spin by Pauli, tried a creative way of obtaining the square root. This resurrected an otherwise unheard of form of algebra called Clifford algebra.
Clifford algebra involves advanced mathematics, and is beyond the scope of this article. For our present purposes, it suffices to say that it gives rise to wavefunction with four components to describe the particle (instead of the usual one in Schrodinger’s theory). These four components describe different spin states of the particle.
The Equation
Once Clifford algebra has been used and required substitutions for simpler units have been made, the equation is of the form
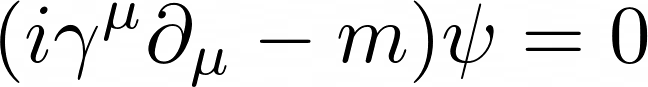
The unusual partial derivative symbol extends for the four components of the wavefunction, i is the imaginary unit and m is the mass.
Implications
The equation was a success in describing behaviour of the electron that the Schrödinger’s equation could not. One such example was that of fine structure of the atomic spectrum. It also helped unify quantum mechanics with special relativity.
One of its most unexpected results was the discovery of antimatter. As the energy expression seen is above is a square, it can have both negative and positive square roots. The positive square roots could be explained, but what of the negative ones? Their existence caused problems as electrons could switch from positive to negative states and release energy, something that was not observed in nature.
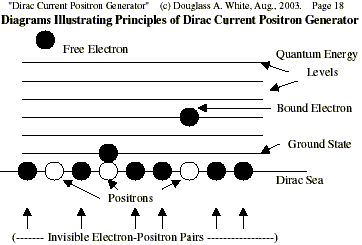
Dirac explained this in 1930 by developing his theory of a sea of electrons, in which absences (“holes”) were visualized as the negative energy carriers. These holes were later predicted to be positrons, the antimatter twins of the electron. In fact, two of the four components of the wavefunction in Dirac’s solution correspond to positron spin states.
Experimental verification of the positron came in 1932 when Carl Anderson confirmed their existence. This paved way for the discovery of the whole series of antiparticles, the antimatter equivalents of matter particles.
Conclusion and Ties to Other Parts of Physics
Dirac’s equation is the fundamental one when it comes to fermions, spin-1/2 particles. These include protons, neutrons, electrons, quarks, and their antimatter counterparts. Particles with integer spin (such as 0, 1 and so on) are described by the Klein-Gordon equation, which turned up early in the history of the Dirac equation. It also works well in conjunction with Fermi-Dirac statistics, which are used to study fermions.
In the timeline of physics, Dirac equation is a major milestone as it marked the unification of quantum mechanics and special relativity. It helped further the relativistic understanding of quantum mechanics. It ushered in a new era of high energy physics, and is an important step along the journey to the Standard Model of physics.