Introduction
Fourier series is a mathematical function that is formed by the sum of scaled sine and cosine functions, over an interval. With adjustment of the scales of the sine and cosine functions, it can be used to represent any function over the chosen interval.
Furthermore, if the function of choice is periodic, then the Fourier series can be used to express the function over its entire domain.
If this all sounds too technical, think of the Fourier series is a tool used to approximate.
There are many functions whose properties can be understood better if they are written as a sum of known functions (the sine and cosine functions in this case). Furthermore, using the Fourier series helps us arrive at the solutions of some differential equations, which were much harder to arrive at otherwise.
Index
Historical background
As a form of approximation by sums, there were rudimentary predecessors for Fourier analysis (the broader category of math under which Fourier series falls) as far back as Babylonian times, but the earliest proper use of functions was in the 18th century.
Interestingly, all this early usage originated in the field of astronomy, where the orbits of celestial bodies required some form of periodic analysis. Famous mathematical minds who contributed to these developments included Lagrange and Gauss, who all made use of trigonometric functions in their solutions.
The mathematician whose name got associated with the method, Joseph Fourier, developed it as a tool to solve a problem in physics: the heat equation in a metal plate. Prior attempts of mathematicians to arrive at the solution of this problem were only partly successful, as they could solve it only for the simpler cases involving a simple sinusoidal (or cosinusoidal) behavior of the heat source.
Fourier made the interesting assumption that the behavior of any heat source could be expressed as a scaled sum of appropriately chosen sine and cosine functions, which were solutions in the simpler case. Now any solution could be expressed in terms of these sine and cosine functions.
While it originated in the context of the heat equation, its applications were much more widespread. Soon mathematicians began to use Fourier series in various problems involving differential equations, which involved sinusoidal solutions.
Fourier analysis, the branch of science that deals with arriving at the Fourier series of a given function, became an indispensable mathematical tool. Thus Fourier transforms and Inverse Fourier Transforms, extensions of the Fourier series for continuous cases, were born. These developments ultimately lead to the development of harmonic analysis, a generalization of Fourier analysis to many kinds of periodic functions.
Mathematical description
Fourier series formula
Consider a real function of interest P(x), over an interval L. This function can be expressed as a Fourier series as follows:
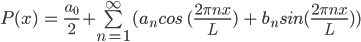
Provided this sum converges in the limit to infinity.
This result is often stated as the Fourier Series formula. However, it does not explicitly state what the coefficients an and bn are. The method for arriving at these is called Fourier analysis, which is detailed below.
Fourier Analysis
The coefficients an and bn are given by the following formulae:
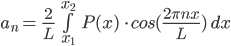
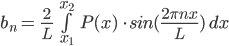
Where x1 and x2 are the end-points of our interval of length L.
Solving the above two integrals gives us the values of the coefficients an and bn which can be substituted in the Fourier series formula in the previous section. Thus, an and bn serve the role of appropriately scaling the sine and cosine functions to represent the function P(x).
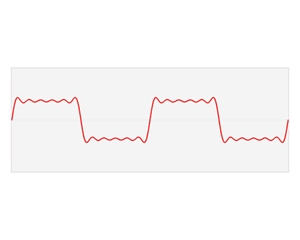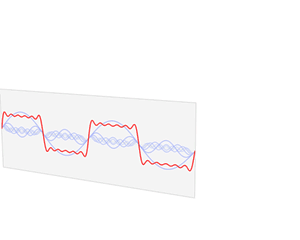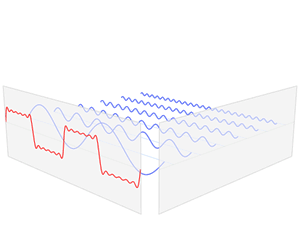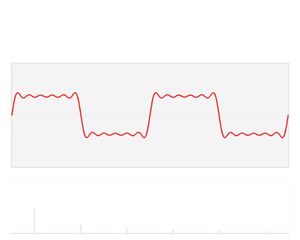
Fourier series in action
Here we consider a simple periodic function, the sawtooth function.
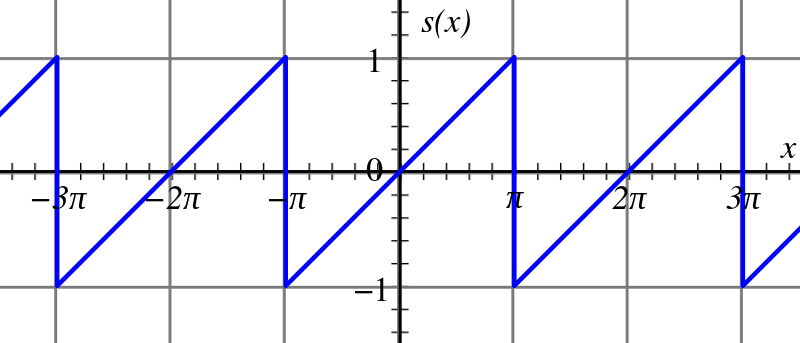
This is the graph of the sawtooth function. What we need now is to obtain the Fourier series of the function. We require firstly the formula of the function, which is:
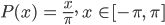
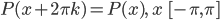
where k is an integer
Now working with the required integrals for the Fourier analysis and substituting L = 2π, we get,
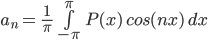
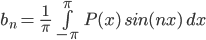
The first of these integrals reduces to 0 because of the properties of the cosine function. The second integral, upon substitution of P(x), and simplification of the resultant integral, yields an answer in terms of n, which gives,
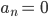
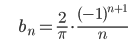
Clearly all cosinusoidal terms (involving an) vanish, leaving us only with sinusoidal terms. Also, the value of bn clearly decreases as n increases (n is in the denominator) and thus the contribution of higher frequency terms reduces.
When substituted back into the Fourier series Formula we get the expression for the Fourier series as:
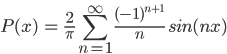
except at the points where x – π = 2πk for any integer k, which is where the function has a jump.
As the formula shows, the sum is taken to infinity, for it to be exact. Finite sums give closer and closer approximations to the sawtooth wave, as the animation below shows.
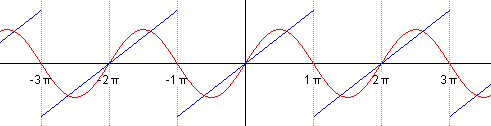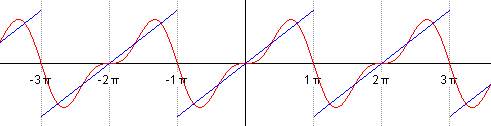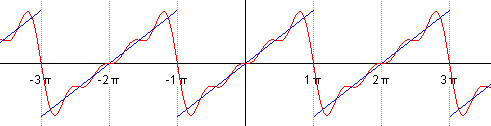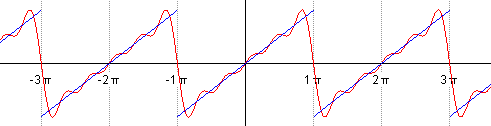
Visualizing this in terms of sines and cosines is abstract, so here is a more concrete visualization involving circles. It is clearly a partial sum, with only a finite number of circles involved. The decreasing radius of the circles shows the decreasing involvement of the higher frequency terms. This corresponds to the lower values of bn as n increases. Even with so few circles, we see that the resultant function on the right (obtained by Fourier analysis) is reasonably close to the actual sawtooth wave.
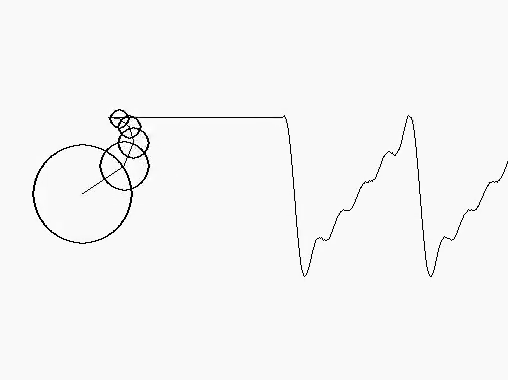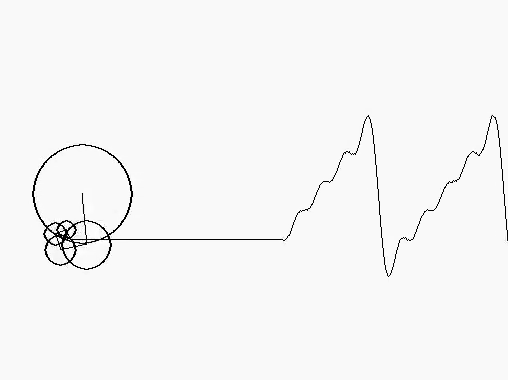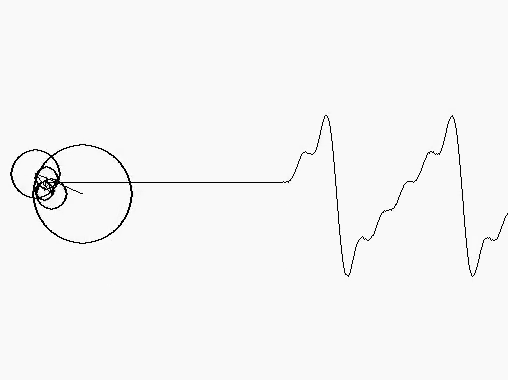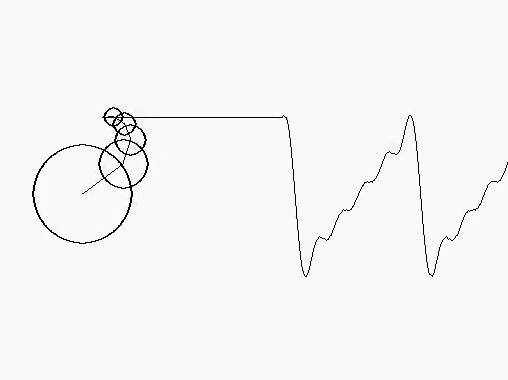
Further scope
One-dimensional real functions are not the only realm of Fourier series. They can be used even in multi-dimensional and complex functions, with appropriate measures taken to account for the increased number of dimensions etc.
While the underlying mathematics is similar in principle, the additional dimensions introduce complexity in the process which goes beyond the aims of this article. It suffices to say that once again the function of interest is written as the scaled sum of sines and cosines, chosen appropriately for the required number of dimensions. Often, the use of Euler’s formula
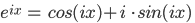
where i is the imaginary unit, is made use of, to simplify notation and calculation, and also deal with complex values if the need arises.
Fourier series, discrete in nature, can also be extended to Fourier transforms and inverse Fourier transforms, which are useful for representing functions as continuous sums (i.e. integrals) of periodic functions.
Applications
Fourier series and their extensions have uses in many fields of mathematics and physics. One of the primary uses occurs in the fields of differential equations, especially certain kinds whose solutions are sinusoidal in nature. The usage of Fourier series makes the route to the solution cleaner and often simpler mathematically. It further provides more clarity on how the solution can be decomposed into its constituent sine and cosine parts.
Fourier series and its extension, Fourier transforms, are extensively used in signal processing, in various digital applications. This is because signals are periodic by nature and thus can be rewritten by the use of the Fourier series formula as a sum of many sine and cosine signals. This makes the signal easier to understand and analyze because its components (sine and cosine signals) can be studied better.
This happens because the Fourier analysis gives a relation between the various frequencies and their scaling factors, and performs a task called spectral analysis, which lets us understand the relationships between various frequencies.
If all this sounds abstract, here are two applications much closer to home.
- Many image editing software use Fourier transforms in two dimensions to perform various actions on the image, such as compression, filtering, and reconstruction. All this is possible because the Fourier analysis lets them understand the image in terms of the frequencies involved in the image.
- Storing sound data in digital formats involves a lot of use of Fourier transforms and series because they pick apart the various frequencies of the sounds and enable them to be appropriately stored in the required manner. This is reflected in the extremely well-compressed nature of mp3 files. This also is used by sound editing software to analyze the various frequencies present in sounds and edit them accordingly.
Conclusion
The Fourier Series is a very important mathematical tool that has its origins in differential equations. Now, however, it has uses in many fields in the world and is indispensable in the digital sector. Indeed, much of the success of signal transmission is owed to the power of Fourier series (and its extension, Fourier transforms), which let us dissect otherwise complicated-looking signals in an understandable manner.

