The Gas Laws

The gas laws are a set of laws and equations that describe the behavior of gasses. It was developed by multiple people over two centuries. 

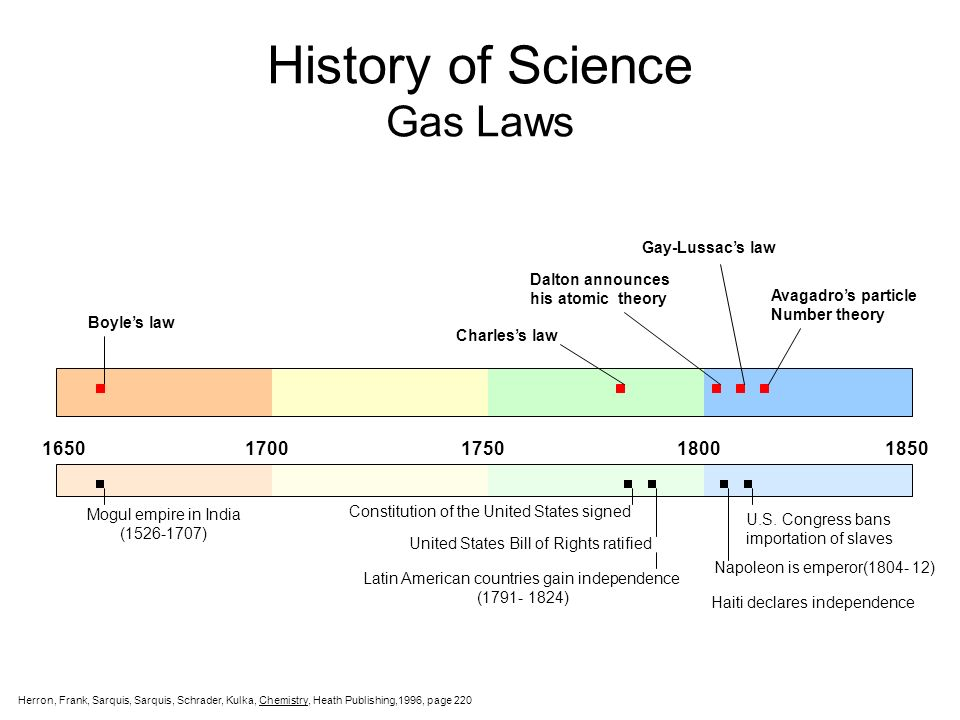
They were developed to provide the relationship between the pressure, volume, and temperature of a sample of a gas. It was found out that it worked as an approximation for all gasses, and a few tweaks could be made to obtain more accurate results. 

Boyle’s Law

The first of the gas laws was published by Robert Boyle in 1662. Boyle’s Law states that:

The absolute pressure exerted by a given mass of an ideal gas is inversely proportional to the volume it occupies if the temperature and amount of gas remain unchanged within a closed system.

This relationship can be expressed mathematically as:

P ∝ 1/V
or
PV = k

where P is the pressure of the gas and V the volume. The non-zero proportionality constant is denoted by k.

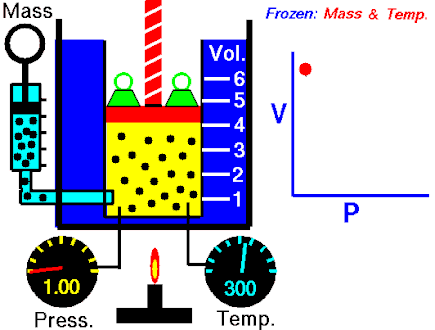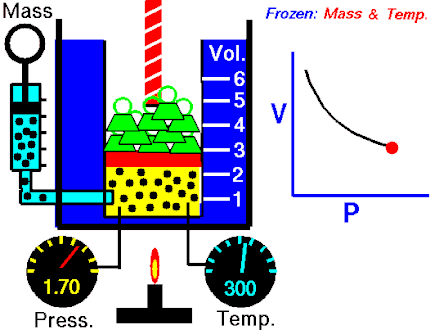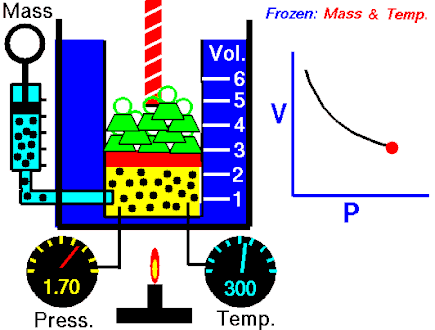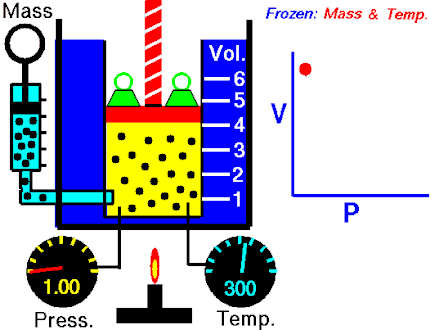
This relationship between pressure and volume was first noted by Richard Towneley and Henry Power in the 17th century. Robert Boyle confirmed their discovery through experiments and published the results. Boyle’s law is based on experiments with air.

The same law was independently identified by the French physicist Edme Mariotte (1620–1684) in 1679. Additionally, he discovered that air volume changes with temperature. Thus this law is sometimes referred to as Mariotte’s law or the Boyle–Mariotte law.

Charle’s Law

After Boyle’s law, the next major discovery was by the French scientist and inventor Jacques Charles in the 1780s. Charle’s Law, which is named after him, says: 

When the pressure on a sample of a dry gas is held constant, the Kelvin temperature and the volume will be in direct proportion.

This law equates the volume and temperature of the gas. Expressed mathematically, this becomes:

V = kT

This can be written as: 

V/T = k

Where, V is volume and T is temperature

Thus, it is possible to compare these values under different conditions using the equation: 

V1 / T1 = V2 / T2

where V1 and T1 are the states at one condition and 

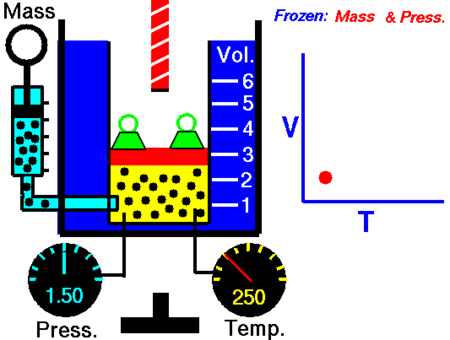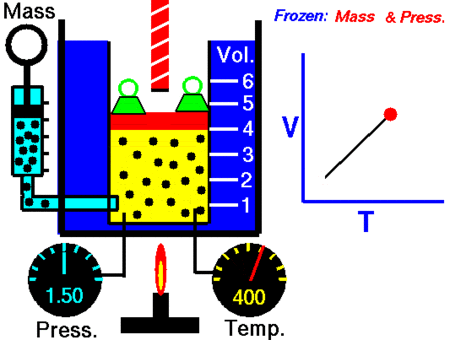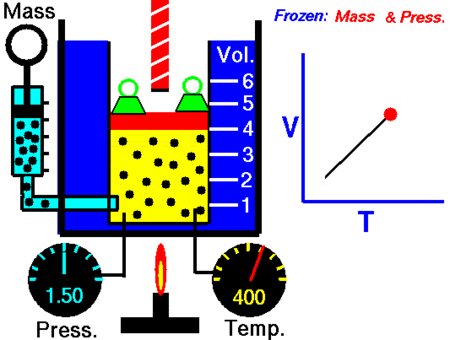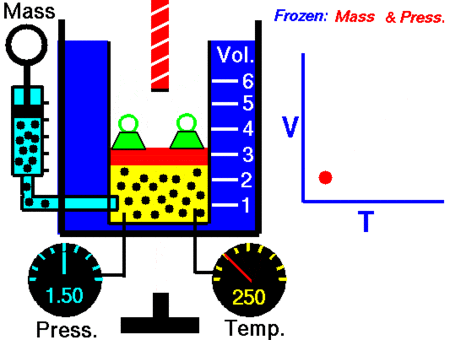
It was John Dalton who demonstrated by experiment that all the gases and vapors that he studied expanded by the same amount between two fixed points of temperature. The French natural philosopher Joseph Louis Gay-Lussac confirmed the discovery in a presentation to the French National Institute on 31 Jan 1802, although he credited the discovery to unpublished work from the 1780s by Jacques Charles. The basic principles had already been described by Guillaume Amontons and Francis Hauksbee a century earlier.

Gay-Lussac’s Law

Speaking of Lussac, he has a law to his name too. Gay-Lussac’s law, sometimes referred to as Amonton’s law,  states: 

The pressure of a given mass of gas varies directly with the absolute temperature of the gas when the volume is kept constant.

Mathematically expressed it becomes: 

P = kT

And like Charle’s Law, the Gay-Lussac’s Law can be used to calculate the pressure at two different points. This law works because the temperature is a measure of the average kinetic energy of a substance; with the increasing kinetic energy of a gas, its particles collide with the container walls more rapidly, hence exerting increased pressure.

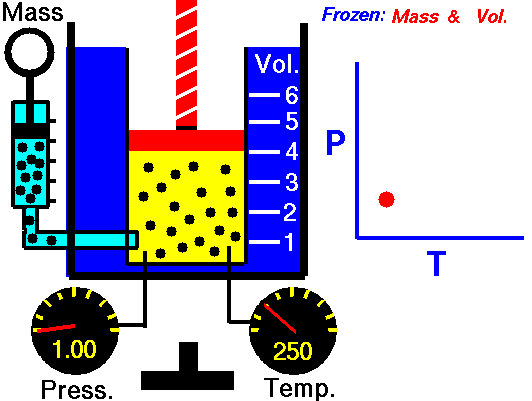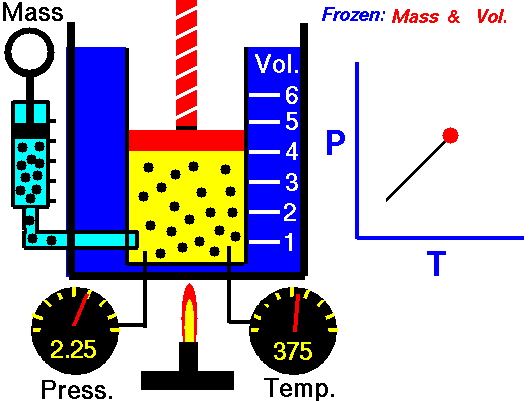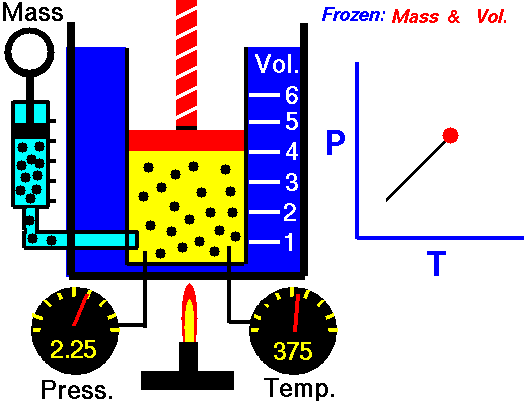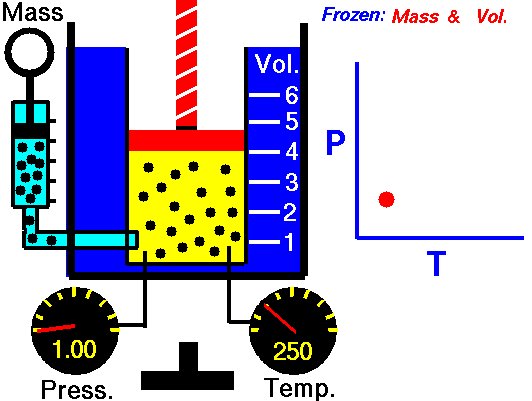
Since Amontons discovered the law beforehand, Gay-Lussac’s name is now generally associated in chemistry with the law of combining volumes discussed in the section above. Some introductory physics textbooks still define the pressure-temperature relationship as Gay-Lussac’s law. Gay-Lussac primarily investigated the relationship between volume and temperature and published it in 1802, but his work did cover some comparison between pressure and temperature.

The Ideal Gas Law

The Ideal Gas Law can be considered a combination of the three gas laws. It is an equation of state for gases and is a good approximation for the behavior of gases under limited conditions.

Mathematically, the law can be expressed as:

PV = nRT

where
P is the pressure of the gas
V is the volume of the gas
n is the number of moles of gas
R is the gas constant, equal to the product of Boltzmann’s constant and Avogadro  number
T is the temperature of the gas.

The ideal gas law can be used in stoichiometry problems in which chemical reactions involve gases. With a little tweaking, it can be used to determine the densities of gases.

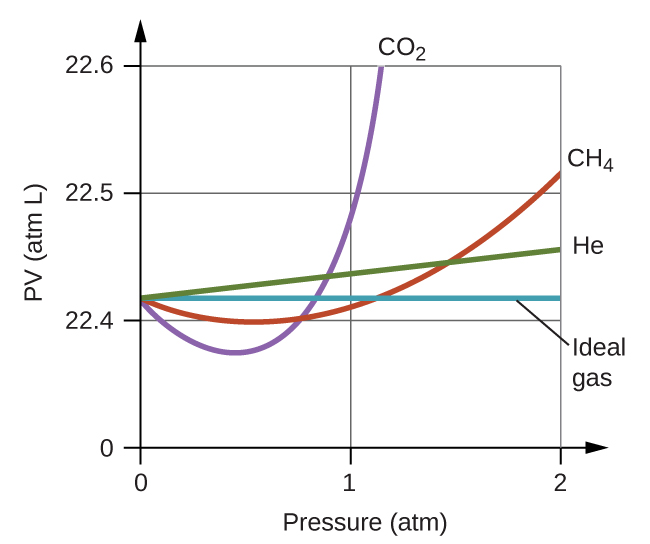
Although the gas law is a good approximation, progress could be made. That is where Van der Waals enters.

The Real Gas Law

The Real Gas Law, also called the Van der Waals equation, is a generalization of the ideal gas law. 

The ideal gas law treats gas molecules as point particles that interact with their containers but not each other, meaning they neither take up space nor change kinetic energy during collisions. To account for the volume that a real gas molecule takes up, the van der Waals equation replaces V in the ideal gas law with (V_m – b), where V_m is the molar volume of the gas and b is the volume that is occupied by one mole of the molecules. This leads to:

P(V_m – b) = nRT

The second modification made to the ideal gas law accounts for the fact that gas molecules do in fact interact with each other and that real gases, therefore, show different compressibility than ideal gases. Van der Waals provided for intermolecular interaction by adding to the observed pressure P in the equation of state a term a/V²_m, where a is a constant whose value depends on the gas. The van der Waals equation is therefore written as:

(P + a/V²_m)((V_m – b) = nRT