Huygens’ principle and the theory he developed, Huygens’ wave theory, were key developments in the establishment of wave optics in the field of physics.
Its major competitor in its years (late 17th century) was Newton’s corpuscular theory, which described light as a stream of particles. Newton’s theory was partially successful, as it could explain the reflection of light. However, it failed to describe most phenomena related to light, such as refraction, diffraction, and interference.
However, Huygens’ theory managed to explain most of these in a better fashion. While the Huygens’ principle originally explained reflection and refraction of light, it was later expanded by Fresnel in the 19th century to explain diffraction.
Thus, it is often called the Huygen-Fresnel Principle. As a result, scientists later acknowledged the Huygens wave theory to be superior when compared to Newton’s corpuscular theory.
The Huygens’s Principle states that every point on a wavefront is a source of wavelets. These wavelets spread out in the forward direction, at the same speed as the source wave. The new wavefront is a line tangent to all of the wavelets.
Index
Introduction
Huygens introduced the concept of a wavefront to explain the wave propagation of light. Think of a light source emitting light in all directions. A wavefront is the set of points where the light has the same phase.
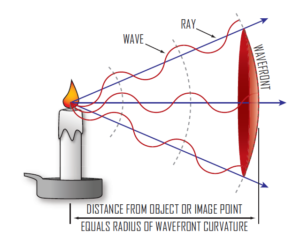
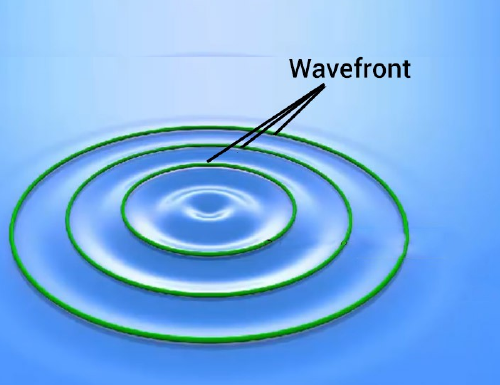
An example which is easier to visualize is that of ripples in water. Each of the concentric circles formed by ripples are wavefronts, as the water particles in them have the same phase.
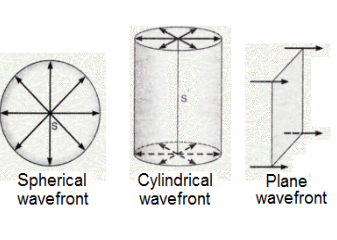
In Huygens’ theory, there are primarily three kinds of wavefronts: spherical, plane, and cylindrical.
Spherical wavefronts are produced by point sources. Plane wavefronts are produced by far-away sources and are in fact approximations of the spherical wavefront. Cylindrical wavefronts are produced by linear sources such as slits.
Basic Premise
Huygens used one simple premise to derive most of the results of his wave theory:
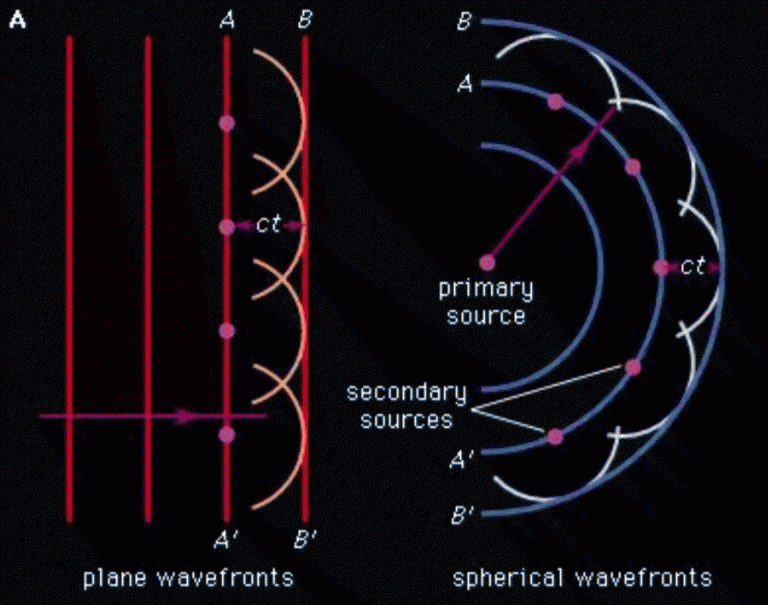
Every point on the wavefront acts as a secondary source of spherical wavefronts. The new wavefront after some time is obtained by adding up the resultant wavefronts from each of these secondary sources.
Here is an animated example of the principle in action, in water waves:
Thus, the basic idea of the superposition of waves was used here, in the context of all the secondary waves. With this simple principle, he could explain the processes of reflection, refraction, and rectilinear propagation of light. However, to do all this, he assumed (without being able to explain yet) that the secondary sources produced waves only in the forward direction.
More clarity was provided by Fresnel who made use of the mathematical concepts of phase and complex amplitude of the waves.
Avoiding a lot of complicated math, we can say that Fresnel’s modifications built upon Huygens’ basic idea of secondary waves, and managed to explain diffraction too. However, Fresnel still could not justify some assumptions he had to make in the derivation. Kirchhoff’s diffraction formula, a mathematical approach helped explain these later.
Huygens Principle in Action
Here is a small animation that shows how the Huygens principle can be used for explaining the refraction of plane wavefronts at a plane surface.

In this figure, to keep it visually simple, we use a limited number of points for generating the secondary waves. As we see, as the plane wavefront goes from the first medium (white) to the second medium (blue) the speed of light changes. As a result, the secondary waves produced in the blue medium are overall oriented at a different angle, because now the spherical wavefronts are moving slower. And hence, the wavefront too changes direction. This explains refraction.
A more mathematically detailed diagram is presented below, and with some geometric knowledge and algebraic manipulation, Snell’s law of refraction can be derived. n1 and n2 are the refractive indices in the two media, and θ1 and θ2 are the respective angles of incidence and refraction.
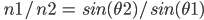
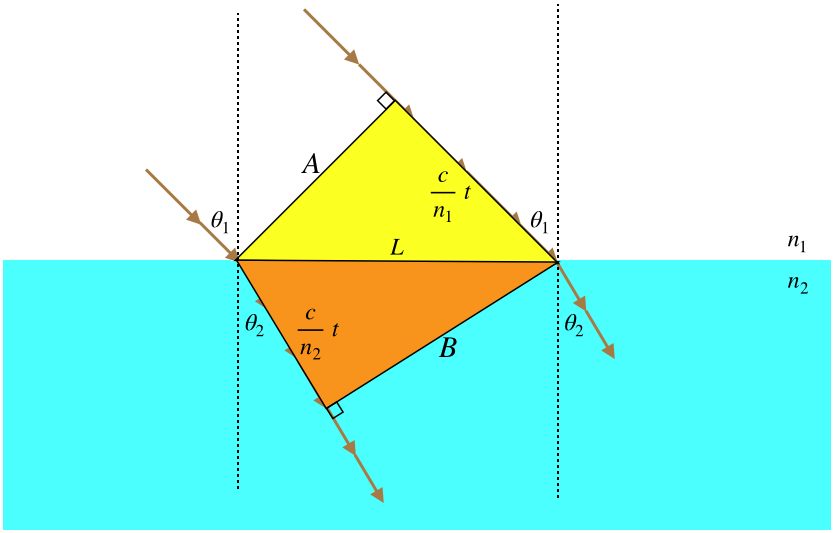
We consider just another example of the Huygens principle in action, to explain diffraction. Plane wavefronts pass through a slit or hole and undergo diffraction.
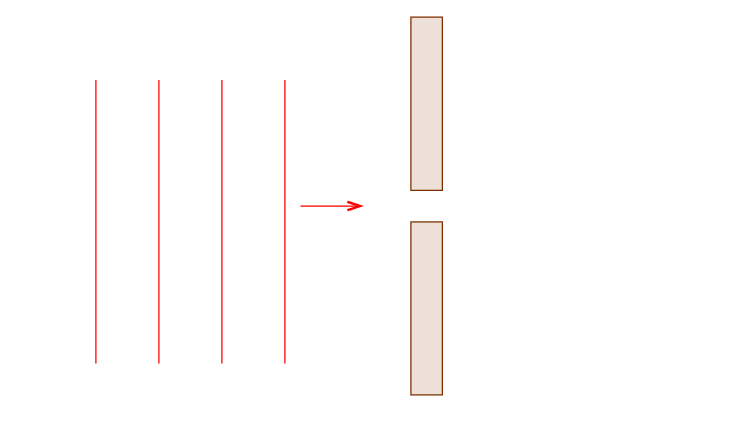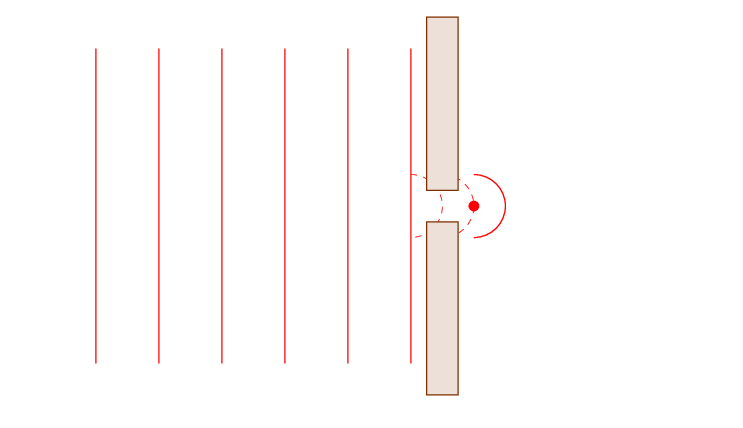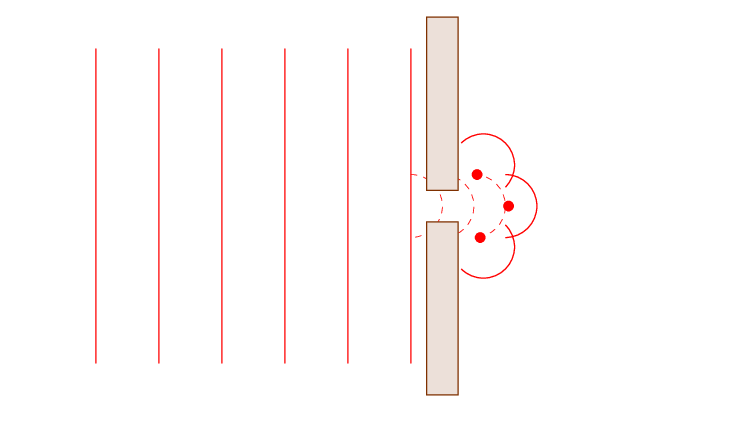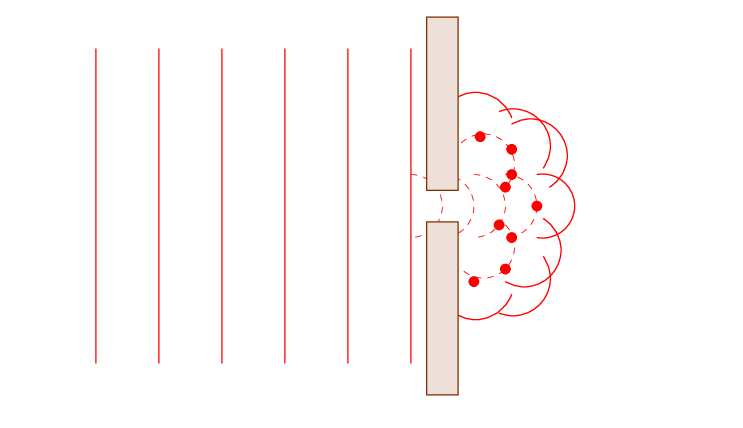
This simplified diagram, while visually easier to observe, might not bring out the beauty of the process, so here is a more continuous animation.
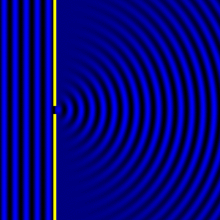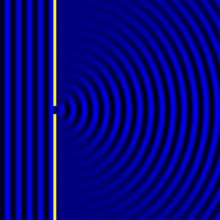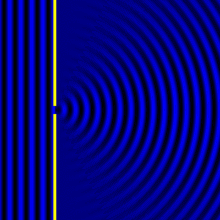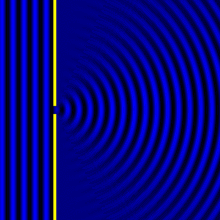
As we see, the plane waves become spherical (or cylindrical) after passing through the hole. This is a 2D representation, so the new wavefronts look circular rather than spherical.
Mathematical Background
To get into some of the mathematical details that Fresnel developed, we consider a complex amplitude of the wave, U. It describes a wavefront that has the usual wave properties of wavelength and frequency. It changes with respect to distance r from source as given by the formula:
U(r) ∝ U0eikr / r
Where i is the imaginary unit and U0 is the initial complex amplitude of the wavefront.
Using this formula for amplitude for each of the points on the wavefront, we obtain a complex integral which must be solved to obtain the new wavefront. While the integral itself is too complicated to be covered here, the important takeaway is:
The use of complex amplitudes in the integral enables the wave amplitude to vanish in certain directions, and thus the Huygens result is obtained, i.e. the secondary waves propagate only in the forward direction.
This was proved more rigorously by the mathematical approach of Kirchhoff as part of his Kirchoff’s diffraction formula.
Position in current physics
While the Huygen-Fresnel principle was very successful in explaining much of wave optics, it was often criticized because the assumptions made (such as secondary waves propagating only in the forward direction) felt arbitrary and could not be explained satisfactorily. Kirchhoff’s mathematical derivation settled some of these doubts.
Later, with the development of Maxwell’s equations and the understanding of the dual nature of radiation and matter, Huygens wave theory came to be seen as an approximation of Maxwell’s theory in homogeneous space.
While it is now theoretically less fundamental than Maxwell’s equations, it still is a useful tool to make calculations in most cases. It still can be used in the modern quantum field theory to explain the behaviour of wavefunctions in homogeneous space.
Conclusion
Huygens wave theory is a very important step in the development of wave optics and a useful tool for making many calculations related to waves. Even if it is theoretically superseded by quantum approaches nowadays, it is an important part of the history of optics. Understanding it is vital for students to optics to appreciate the development of the field.

