The Young’s Double Slit experiment was one of the most important experiments of physics. It was conducted by Thomas Young in 1801. At that time, although Huygens had shown that light has a wave nature with Huygens’ experiment, the reputation of Newton was such that light was still considered to be a beam of particles. It was this experiment that managed to convince the scientists of the time that light does behave like a wave.
Index
The Assumptions Made
There are three assumptions made to obtain the mathematics involved in this double slit experiment.
- The light source used is coherent, that is, it has a constant wavelength and constant phase difference.
- The distance between the two slits is much smaller than the distance between the slits and the screen.
- The distance between the slits is large relative to the wavelength of the light used.
Mathematically, this can be boiled down into:
- D >>> d, thus the light rays can be approximated to parallel rays.
- d >>> , where is the wavelength of the light used.
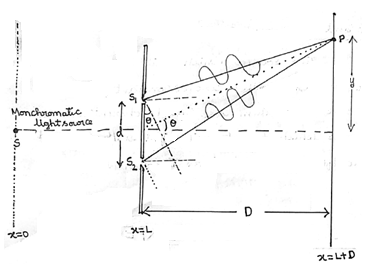
Thus from the diagram, the approximation, sinΘ ≈ tanΘ = y/d can be made. And so, the path difference becomes Δz = y/d .
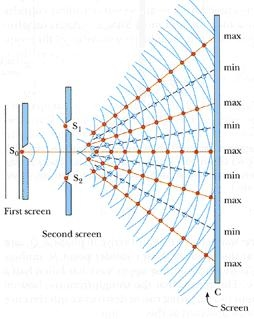
The Experimental Setup
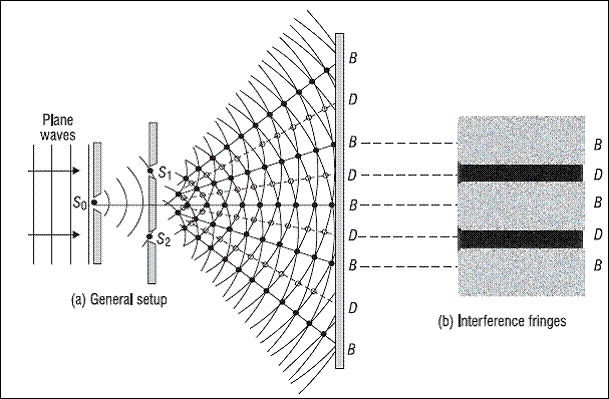
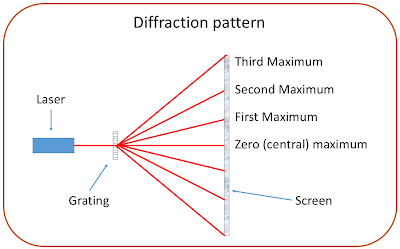
The setup is given by the diagram below. Light from a monochromatic coherent source of light is allowed to pass through two slits, and then fall on a screen.
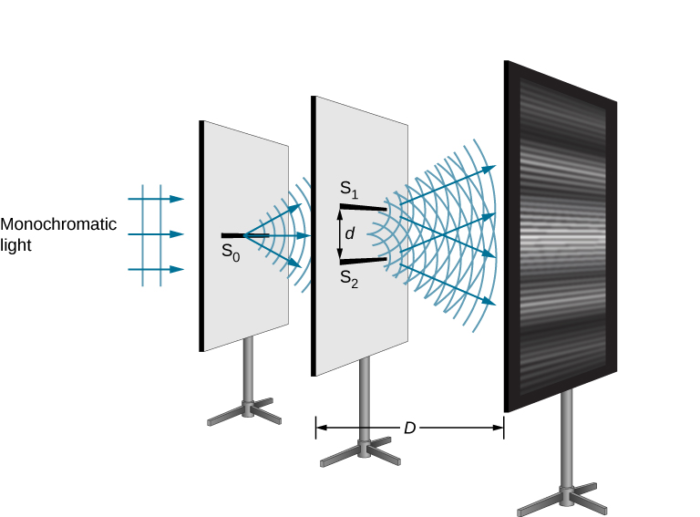
If Newton’s corpuscular theory had been applied here, what you would expect to see are two bands of light, one on each slit. But the experiment showed something different which couldn’t be explained by the particle theory of light.
On the screen, bright and dark fringes are observed. This is because of the phenomenon of interference of light, which reflects the wave nature of light.
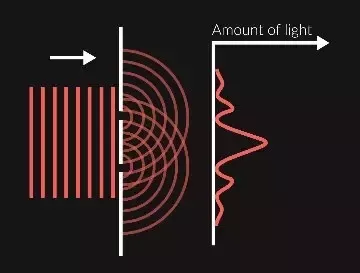

The patterns can be explained based on constructive and destructive interference. But this would imply a wave nature. In the future, thanks to the work of Einstein and Plank, the dual nature of light was established.
The Mathematical Explanations
The derivation of these equations is done on the principle of the superposition of waves. Here, we will look at a few major aspects.
Position of the bright fringes
Bright fringes occur when constructive superposition occurs. Therefore, for a bright spot to be observed at point P, the path difference Δz required is:
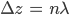
where n is an integer. Thus, from the diagram, the path difference can be written as:
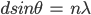
Thus, the position of bright fringes can be obtained by substituting the value of sinΘ in the equation and simplifying, we obtain the equation:
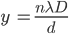
where y is the distance of the fringe from the centre of the screen, n is an integer, Λ is the wavelength of the light and d is the distance between the slit.
When n = 0, a bright fringe is observed at the centre of the screen. This is called the Central Maxima. The other bright fringes are arranged symmetrically with respect to the central maxima.
Position of Dark Fringes
The dark fringes occur when there is destructive interference. For this to occur, the following condition for the path difference is required:
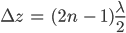
where the symbols retain the same meaning as of the previous subsection. Upon simplification, the following formula is obtained:
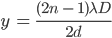
These dark fringes are called minima. The first minima are found next to the central maxima.
Fringe Width
The distance between two bright or dark fringes is called the fringe width.
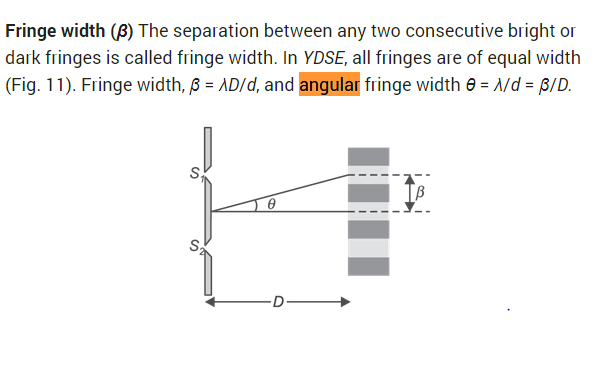
With the equations of the maxima and minima, the fringe width Β (beta) can be identified by the equation:
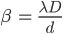
which is obtained by subtracting the nth and the (n-1)th of either the maxima or the minima. Similarly, the angular width can be derived, and the formula obtained is:
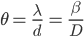
Thus, we can see that while the fringe width depends on the distance from the slit to the screen, while the angular fringe width is independent of that parameter.
In Present Day
There have been studies in the field of nanoplasmonics, wherein they studied the interaction between the particles at the nanoscale. The findings may be useful in the emerging areas of nanoantennas.
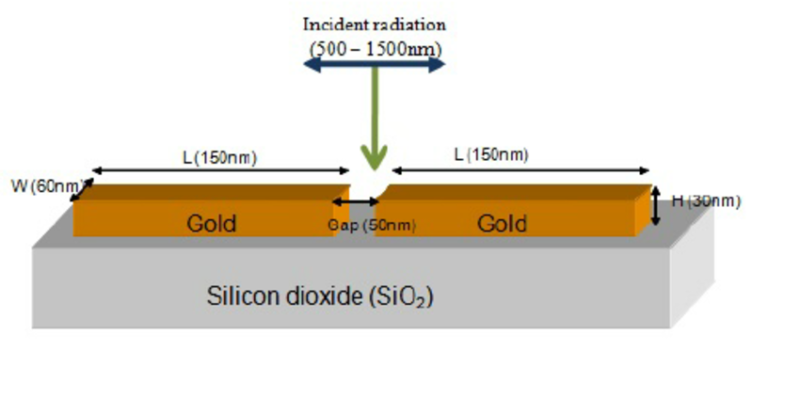
So, that was all about Young’s Double Slit Experiment.

