Poisson’s Equation

Poisson’s equation is a partial differential equation that has many applications in physics. It helps model various physical situations. Knowing how to solve it is an essential tool for mathematical physicists in many fields.

The Mathematical Statement

Mathematically, Poisson’s equation is as follows:

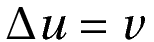
Where
Δ is the Laplacian,
v and u are functions we wish to study.

Usually, v is given, along with some boundary conditions, and we have to solve for u. A special case is when v is zero. This is called Laplace’s equation

In common applications, the Laplacian is often written as ⛛². The choice of which coordinates to expand the Laplacian depends on the conditions of the problem.

Solving the Equation

The Poisson’s equation is a linear second-order differential equation. This means that the strategies used to solve other, similar, partial differential equations also can work here.

One popular method used is Separation of Variables. To use this, we must simplify the Laplacian. If we are dealing with more than one dimension, this can be done by using suitable coordinate systems. Then, if we expand the Laplacian, we can assume a variable separable solution. The final solution then can be attempted by solving for each of the coordinates separately. It is important to make sure that the solution meets the boundary conditions.

Another, more general solution uses the Green’s function. This is a function that is defined to satisfy the Poisson equation at specific points in space. Then a total solution can be arrived at by taking together different solution with appropriate weights.

When such analytical methods cannot give exact solutions, we use numerical methods to arrive at approximate solutions. These often use looping algorithms. The algorithm usually starts with a trial solution and is improved on each repetition of the loop.

Occurrences in Physics

Conservative Forces

One situation in which Poisson’s equation turns up often is the case of conservative forces, or fields. A conservative field F can be written as the gradient of a potential ϕ.

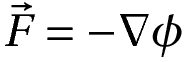
At the same time, the field is related to some other quantity ρ as its divergence.

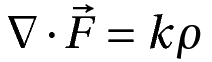
where k is some constant.

Using the above two equations, we get a Poisson’s equation, which is:

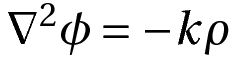
The specific case determines the identity of the functions ϕ , ρ and F.

Electrostatics

In the case of the electrostatics, ρ corresponds to charge density and F is the electric field E.

In the special case of the electric field being conservative,ϕ  becomes the electric potential. Specific solutions depend on how the charge density is distributed.

Dealing with the limiting case of a lone point charge, we get an expression that can be derived from Coulomb’s law.

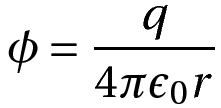
where charge q takes the place of charge density ρ

Gravity

The logic is similar here, except we get gravitational potential and fields instead of the electrostatic versions. Mass density replaces charge density. Again, in the special case of a point mass, we get an expression that relates to Newtonian gravity.

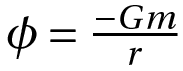
where
m is the mass
G is the gravitational constant.

In Other Situations

Poisson’s equation also turns up in other regions of physics as well.

Heat Flow

We can model Heat flow using a second-order partial differential equation. This is written as:

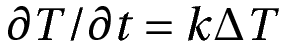
This becomes into the form of the Poisson’s (or Laplace) equation when the left hand side is a constant (or zero). This corresponds to steady change in temperature. We can then solve for the temperature T based on boundary condition.

Navier-Stokes Equation

Parts of the Navier-Stokes equation, which deal with fluid flow, take the form of the Poisson’s equation in some specific cases. The same logic used in the previous cases will be extended here with modifications.

FAQ