The modern understanding of the atom emerged in the early 20th century. The Quantum Mechanical Model of the atom was a major breakthrough in this process. It was a radical shift in thinking and helped scientists gain a more comprehensive understanding of nature. It now explains not just microscopic systems, like atoms, but also large-scale occurrences like superconductivity.
Index
Beginnings
The dominant theories of the late 19th century were what we now call “classical” theories. They had been very successful in describing everything scientists had studied so far. Scientists then were confident that the understanding of the universe was more or less complete.
“There is nothing new to be discovered in physics now. All that remains is more and more precise measurement.” quoted Lord Kelvin, a prominent physicist
However, things turned out to go very much against these expectations in the late 19th and early 20th centuries. Many experiments began giving results that went against classical physics. These came to be known as the failures of classical physics.
Wave-particle Duality
At the heart of the failures of classical physics was wave-particle duality. According to classical physics, waves and particles were independent. Radiation, such as light, was in the form of waves. Matter, like electrons, protons, and all else around us, was in the form of particles. There was no overlap.
However, the results of some experiments showed that radiation could sometimes act as a collection of particles. Such experiments include the photoelectric effect and the Compton effect. Both the experiments showed that light was a stream of particles (photons) instead of a wave.
Similarly, there were experiments that showed that matter could display wave nature. An example is the electron diffraction experiment of Davisson and Germer in the early 1920s. It showed that electrons can behave similarly to waves in some crystal diffraction studies.
The result of all these experiments was simple: the line between wave and particle was very blurry and depended on context. This would turn out to be important for the quantum mechanical model because electrons would show wave-like properties in that context.
Quantization
The word ‘quantum’ means a small amount. The reason why quantum mechanics is so different from classical physics is because of the phenomenon ‘quantization’. This means that some measured values come in fixed steps, instead of smooth continuous amounts. For visualization, compare a staircase with a ramp. The staircase matches the quantum case, while the ramp is the classical case.
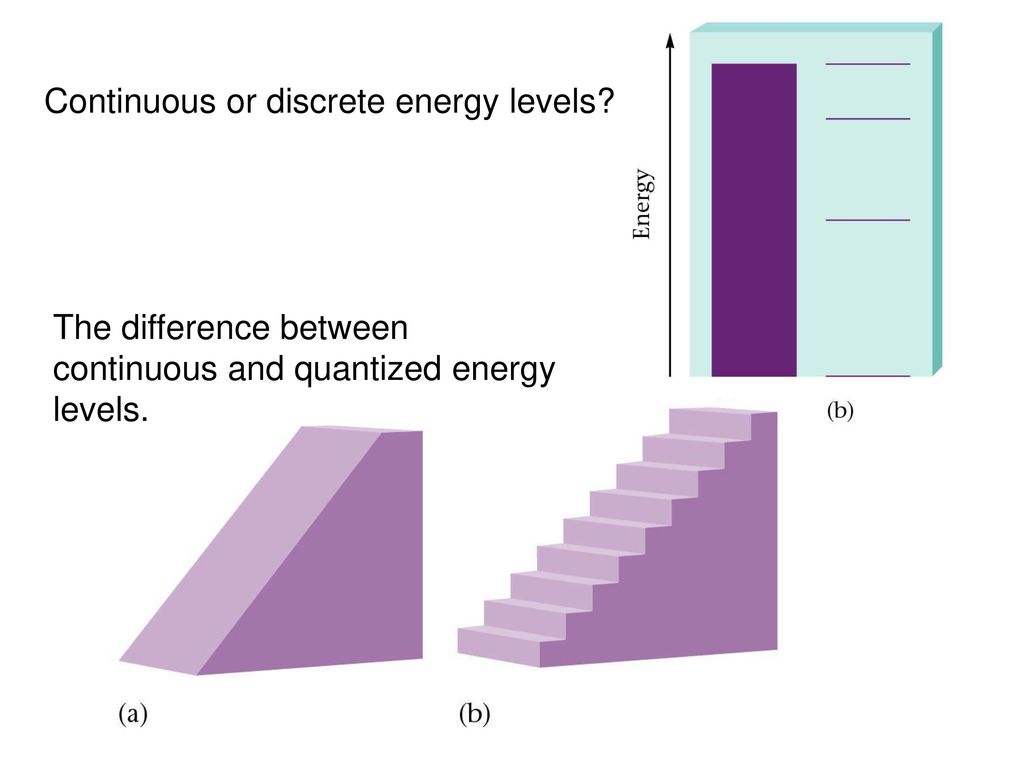
One of the earliest uses of quantization was in Planck’s explanation of black body radiation (another failure of classical physics). It soon emerged that many important physical variables such as energy and angular momentum take values in fixed steps, not continuous values. This was another step towards the development of the quantum theory. This is because, in the quantum mechanical model, one must account for the electrons having discrete energies.
Uncertainty
As we have seen so far, several previously ‘solid’ foundations of classical physics were shaken by their experimental failures. One of the most stunning new ideas was that of uncertainty. Previously, physicists used to think that the only limit on measurement is the tool. That is, with a precise enough tool, one can measure the required quantity with as much precision as we want.
However, the Uncertainty Principle, as put forth by Werner Heisenberg, stated that it was physically impossible to achieve more than a certain amount of certainty.
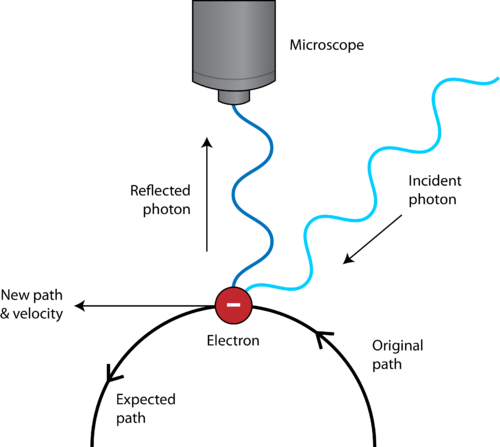
In other words, the act of measuring disturbs the system, so we can never be sure of the exact values. Thus, the classical idea of a path or trajectory disappears.
In a quantum mechanical model, there can be no definite path as every measurement changes the properties of the system.
Quantum Mechanical Model of the Atom
Predecessors
The most prominent predecessor of the quantum mechanical model of the atom was Rutherford’s model of the atom. It said that atoms are composed of electrons orbiting nuclei, similar to planets and the sun. However, it had an obvious flaw: it did not explain how the atoms are stable. According to classical physics, accelerating particles lose energy. This should make the orbiting electrons crash into the nucleus really fast.
An improvement was Bohr’s model. It used concepts like quantization of angular momentum and managed to partly explain the atomic structure. Bohr’s Model suggested that there are certain specific orbits called ‘stationary states’ or ‘shells’, where the electrons do not radiate energy. It also managed to explain some characteristics of atomic spectra.
Schrodinger’s Equation
The Quantum mechanical model of the atom took off with Schrodinger’s equations.
Schrodinger took a new perspective of the atom in the 1920s. He assumed that electrons can be described by a mathematical concept called a ‘wavefunction‘. Then, by using the results obtained from the failures of classical physics, he developed an equation, now known as Schrodinger’s equation.
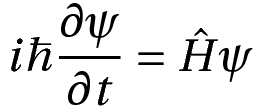
Where,
Ĥ corresponds to the Hamiltonian, an operator
ψ is the wavefunction
ħ is the reduced Planck’s constant.
This equation is basically a partial differential equation. One needs to know about the energy of the system and its potential energy, as well as the initial state of the system. Once these are known, the solution will give the values of the wavefunction for future times.
Interpretation
Solving the Schrodinger’s equation for the simplest case of the hydrogen atom gives specific wavefunctions. Later, Max Born gave physical interpretation for these wavefunctions. Simply put, the absolute square of the wavefunction at a point gives the probability of finding the electron there.
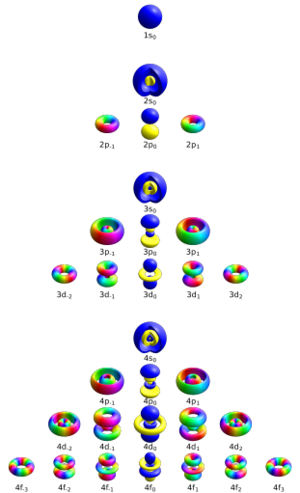
Comparing the wavefunctions of the quantum mechanical model to the stationary states of Bohr’s model, scientists realized correlations. The so-called ‘shells’ corresponded to regions of maximum probability of finding the electron.
We can see that the new quantum mechanical model captures uncertainty very well. The electron does not have a well-defined position, velocity or orbit. We just have a probability of finding an electron in an area.
The familiar chemical concept of ‘orbitals’ also arises from these wavefunctions. Orbitals are regions within which there is a reasonably high chance (~95%) of finding the electron. Suitably integrating the squares of the wavefunction over 3-d space gives orbitals.
Conclusions
The quantum mechanical model of the atom came after years of failure of classical physics. It takes a more modern view of electrons, as particles that are described by wavefunctions.
As a result of its development, scientists have a more nuanced view of reality, as described by the wave-particle duality.
The model was extended to heavier atoms as well. The results show remarkable agreement with theory. Overall, it is part of the larger theory of quantum mechanics, that helps understand phenomena at the smallest level.

